IMPLICAZIONI

. Se stimiamo un processo DSP come se fosse un process TSP sviluppiamo regressioni spurie perchè y t and t are non-stationary.

. I residui da questa regressione non saranno stazionari (capiremo meglio dopo).

. Strada intrapresa dopo l'individuazione dei problemi legati alla stima con variabili non stazionarie first-differenciation

PROBLEMI

. i) L'errore nella stima con le variabili differenziate non è white noise;

. ii) Si perdono importanti informazioni legate ai livelli delle variabili (vedremo bene con la cointegrazione)

NB: PERCHÈ PARLIAMO DI RADICI UNITARIE?

Per capire per quale ragione parliamo di radici unitarie dobbiamo riferirci al concetto di radice di un polinomio generico. Si consideri un semplice processo AR(1) generico:

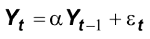
e lo si rappresenti con l'operatore ritardo L

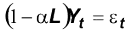
Sotto quali condizioni questo processo stocastico sarà stazionario?

Se la radice dell'equazione: (1-αL)=0 è maggiore di uno (in modulo).

Ora, poichè la radice dell'equazione è: L= 1/ α

sappiamo che la radice è maggiore di uno se e solo se: -1< α <1

Nel caso limite di α=1 il processo stocastico NON E' STAZIONARIO [CASO (già visto) DEL RW]

Prof. Paolo Mattana

Successivo: Non stazionarietà delle serie temporali III

Sommario: Index