Il test Dickey-Fuller

. Abbiamo già discusso dei pericoli legati alla mancata (corretta) detrendizzazione delle serie;

. E' importante impare a discriminare tra serie I(0) e I(d);

. Test informali (funzione di autocorrelazione);

. Test formali (ADF, PP..molti altri);

. Noi studieremo solo il test Dickey-Fuller (DF, ADF).

Il sistema della ipotesi è:

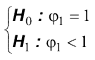
in un modello AR(1) (con o senza componenti deterministiche)

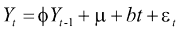
Sotto H ₀ Y contiene una UR (cioè possiede un trend stocastico)

Sotto H ₁ Y è trend-stationary (cioè possiede un trend d eterministico)

Il modello è (di solito) riparametrizzato:

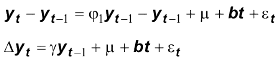
dove γ = ( φ 1 - 1), e il sistema delle ipotesi è ri-espresso come:

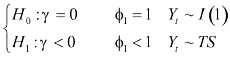
Ci sono tuttavia due complicazioni importanti:

1. La statistica t relativa a g non segue la distribuzione usuale

2. Il processo AR che genera la serie può essere di ordine superiore

Questa è la forma della distribuzione

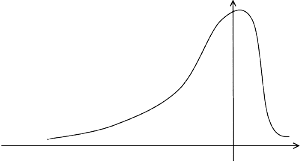
Inoltre, poichè:

1. Il test discrimina a sinistra (test ad una coda)

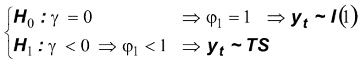
2. e la distribuzione è asimmetrica

i valori critici (in valore assoluto) saranno maggiori di quelli di una distribuzione t regolare

IL TEST DICKEY-FULLER AUMENTATO

Il secondo problema riguarda il fatto che la regressione DF è derivata prendendo in considerazione un semplice processo AR(1);

Nel caso generale di un processo generico AR( p ), la regressione ausiliaria necessita di ulteriori p ritardi

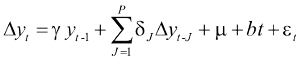
Solo allora possiamo imporre la restrizione γ = 0;

Questo test è chiamato Augmented Dickey-Fuller (ADF) test

Prof. Paolo Mattana