Abbiamo già discusso il fatto che: esistono 2 motivi (principali) che possono portare a E( ee' )≠ s 2 I
- Gli elementi lungo la diagonale principale possono variare;
- Gli altri elementi possono non essere tutti zero.
- Il problema della non-constanza della varianza dell'errore è conosciuto come HETEROSKEDASTICITY
- Il problema delle covarianze non nulle degli errori è conosciuto come AUTOCORRELATION
- Sono problemi differenti che nascono in contesti diversi (dati di natura diversa)
- Le implicazioni per le proprietà degli stimatori OLS sono le stesse
Le cause dell'eteroschedasticità
- E' un problema che si trova in dati cross-section (specialmente dati aggregati);
-L'accuratezza delle misurazioni può differire tra le unità prese in considerazione;
- L'errore può essere proporzionale alla grandezza dell'unità presa in considerazione (esempio GDP).
..abbiamo già visualizzato nel modello bivariato
Le cause dell'autocorrelazione. Nasce nelle time-series
--> E' possibile anche l'autocorrelazione nelle cross section. Si parla allora di correlazione "spaziale" che ha un significato preciso ed è difficile da trattare
- Errori di misurazione (autocorrelati)
- Struttura dinamica
- Forma funzionale errata (non genuina)
..abbiamo già visualizzato nel caso bivariato
Proviamo a generare una serie artificiale autocorrelata
Cosa succede se abbiamo una violazione delle assunzioni sul comportamento dei disturbi?
NB: la matrice ee' non si conforma alle ipotesi classiche
Lo stimatore OLS:

non è coinvolto e continua ad essere lineare - corretto - consistente
La varianza e lo S.E. del coefficiente sono invece coinvolti. Si ricordi che avevamo dimostrato che:

Dobbiamo studiare la matrice var/cov dei beta
Definizione: La matrice Var./Cov. dei beta ha la seguente forma matriciale:
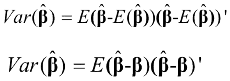
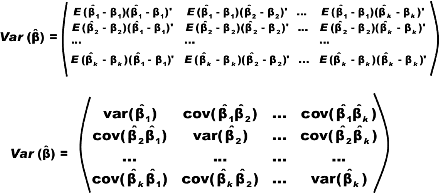
Come possiamo formare gli elementi della matrice? Sappiamo che:
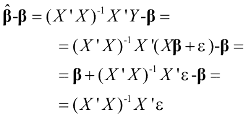
Come possiamo formare gli elementi della matrice? Sappiamo che:
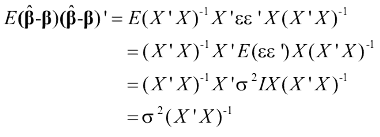
Da cui:
a) non possiamo utilizzare le procedure inferenziali viste fin qua;
b) OLS non è più BLUE;
c) Dobbiamo ricorrere alle procedure GLS che stimano
(ß*)=(X' V - ¹X) - ¹X' V - ¹Y
(che è lo stimatore BLUE del vettore ß vero della popolazione)
Tuttavia V non è conosciuta. La si deve stimare:
Abbiamo a che fare con Feasible Least Squares
NB: Le stime GLS implicano una trasformazione del modello di regressione lineare.
Ne studieremo diverse: Cochrane-Orcutt per il caso dell'autocorrelazione; WLS per il caso dell'eteroschedasticità.
Prof. Paolo Mattana
Successivo: Le procedure GLS di trasformazione
Sommario: Index