L'idea CBT è quella di stimare 2 regressioni separate per 2 sub- campioni e di vedere se esistono "differenze significative". Come si svolge il test? Dividere le osservazioni in 2 sottocampioni (ciascun sottocampione deve contenere più osservazioni di regressori). Nella versione F, il test confronta:

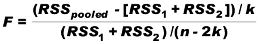
Dove RSSpooled è riferito al modello ristretto ( "pooled", condotto su tutte le osservazioni), RSSi è riferito al sub-campione i, n è il numero di osservazioni, k il numero di regressori

Problema principale:

Servono molte osservazioni in tutti i sub-campioni (es: structural change da periodi di pace a periodi di guerra per i quali sono possibili poche osservazioni). il Chow forecast test, dovrebbe essere usato in questi casi

IL PREDICTIVE FAILURE TEST

Il "Chow test for predictive failure" stima il modello in un sub- campione (comprendente la prima osservazione). Il modello stimato è utilizzato per predire i valori della variabile dipendente. Nella versione F abbiamo:

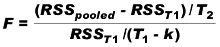
dove RSS pooled si riferisce a tutte n le osservazioni, RSS T1 alle T1 osservazioni del sub-campione. Equivalente a supporre T2 dummy observation specific "ristrette a zero"

STAGIONALITA'

. Spesso le serie temporali esibiscono una qualche periodicità (chiamata stagionalità);

. ES: I dati trimestrali di vendite al dettaglio tendono ad avere un picco nel quarto trimestre;

. La stagionalità può risolversi aggiungendo un set di dummy in corrispondenza dei trimestri (mesi). Come saranno fatte le dummy in questo caso?

STABILITA'

Recursive Least Squares

Le stime RLS consentono di verificare la stabilità dei parametri.

Le equazioni sono stimate ripetutamente.

- i) si stima con le prime k+1 osservazioni ( k numero dei regressori)

- ii) si plotta il primo beta;

- iii) si stima con k+1...e così via

Definizione correlata: recursive residuals

- In corrispondenza di ciascuna nuova previsione di beta, si può cercare di predire il valore della variabile dipendente. The one-step ahead forecast error (opportunamente normalizzato), è un "recursive residual".

- Definizione utile per verificare la presenza di "cambiamento strutturale"

CUSUM TEST

CUSUM^2 TEST

CUSUM Test Il test CUSUM (Brown, Durbin, and Evans, 1975) si basa sulla somma cumulata dei residui ricorsivi

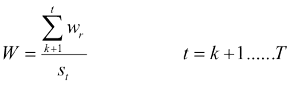
Se non ci sono cambiamenti strutturali, il valore atteso della statistica è zero. Altrimenti tende a fuoriuscire dalle bande di accettabilità. (Cfr. test in Eviews)

CUSUM of Squares The CUSUM of squares test (Brown, Durbin, and Evans, 1975) si basa sulla statistica

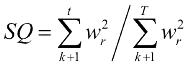
Il valore atteso sotto H0 del CUSUM^2 varia da zero a uno. Anche qui esistono bande di accettabilità

Prof. Paolo Mattana

Successivo: Non stazionarietà delle serie temporali

Sommario: Index