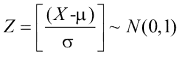
Esempio 1 : se Z = 1.96 calcolare P ( Z > 1.96) Þ 0.025;

Esempio 2 : calcolare P (0 < Z < 2) Þ 0.4775;

NB: E' possibile ulteriormente semplificare i calcoli usando la rete..

Link divertente: http://davidmlane.com/hyperstat/z_table.html

Esempio 3: si assuma X ~ N (10, 4). Trovare P (8 < X < 12).

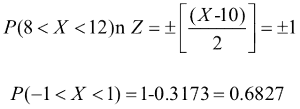
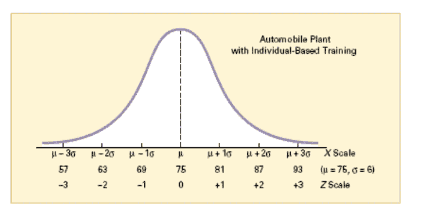
LA NORMALE STANDARDIZZATA

LA CORRELAZIONE FRA VARIABILI CASUALI

Esistono diversi metodi per misurare la relazione esistente tra due variabili

- Analisi di correlazione

- Analisi di regressione (più complicata)

- L'analisi di correlazione è semplice ma, purtroppo, non aiuta a capire la natura della relazione tra le variabili.

La correlazione semplice misura "l'intensità" di una relazione lineare esistente fra due variabili (in un diagramma di dispersione i punti tendono ad accumularsi su una retta immaginaria). Già dalla vicinanza dei punti attorno ad una retta (curva) si può giudicare la forza della correlazione tra una variabile e l'altra.

Esempio: si scarichino i dati su reddito e consumo da istat.it e si costruisca un diagramma di dispersione con i tassi di crescita delle due variabili

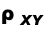misura la correlazione tra X e Y

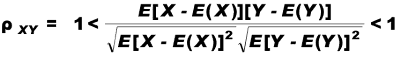
Il numeratore si chiama covarianza tra X e Y

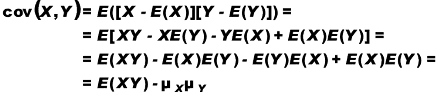
Esempio:

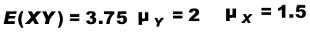
Cosa significa avere una covarianza di 0.75?

Esiste una relazione positiva (lineare) tra X e Y

- positiva perché la deviazione dalla media tende ad avere lo stesso segno nelle due variabili

- Lineare

NB: per mezzo della covarianza non so apprezzare l'intensità della relazione lineare

La correlazione è invece un numero "puro" compreso fra 1 e -1

Prof. Paolo Mattana

Successivo: Il processo di inferenza statistica

Sommario: Index