Problema dell'inferenza: cosa sappiamo dire sulla popolazione partendo dal campione?

NB: Se il campione riproducesse esattamente i singoli momenti della popolazione di appartenenza la soluzione al problema dell'inferenza sarebbe facile da risolvere. Poiché, invece, ciò non accade sono necessari accorgimenti "tecnici" per capire e utilizzare le informazioni derivabili dai campioni. In particolare, sappiamo "molto" su come si comportano i momenti principali dei campioni rispetto ai corrispondenti valori delle popolazioni

Il nostro problema sarà quello di "fare inferenza" sui parametri della popolazione (a noi sconosciuti) sulla base delle osservazioni campionarie. Come possiamo operare? Abbiamo tre diverse livelli di intervento. Possiamo richiedere:

. una stima puntuale dei parametri della popolazione ( point estimation );

. una prob. che tali parametri si collochino entro due valori limite ( interval estimation );

. un'indicazione prob. sul fatto che un particolare parametro della popolazione esibisca determinate caratteristiche ( hypothesys testing ).

Point estimation

Costruiamo una funzione delle osservazioni chiamata stimatore.

Stimatore: variabile casuale che rappresenta il nostro "miglior" tentativo di catturare il valore vero appartenente alla popolazione.

Come costruiamo stime puntuali? Esempi di inferenza univariata: come faccio a inferire il valore della media o della varianza di una popolazione generica?

Esempi di stime puntuali

Abbiamo già visto che Possiamo quindi immaginare di utilizzare la media campionaria come (stimatore non distorto della media (vera) della popolazione). Stiamo, cioè, costruendo una funzione delle osservazioni (stimatore) per "catturare" il valore vero m . La funzione dei parametri (stimatore), in questo caso, è

E' molto interessante studiare le proprietà della media campionaria. Già sappiamo che:

Se infiniti campioni casuali di dimensione n sono tratti da una popolazione generica , allora:

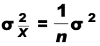
Dimostrazione:

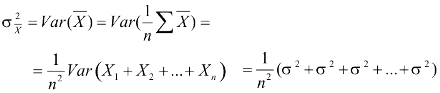
(Che fine fanno le covarianze?)

NB:

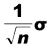è indicato come standard error della media

Prof. Paolo Mattana

Successivo: Teorema del limite centrale

Sommario: Index