Come costruire intervalli di confidenza

Sappiamo che:

. La media campionaria si distribuisce secondo una normale (teorema del limite centrale);

. Per ogni distribuzione normale: il 95% delle osservazioni è compreso all'interno dell'intervallo:

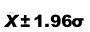
Per le medie, lo standard error (SE) della media è

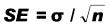
Quindi, il 95% delle medie sarà compreso nell'intervallo:

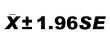
Esercizio 3.5

Gli onorari orari in un campione di 40 studi risultano in media pari a 25$ con s = 3,7. Si ottenga un intervallo di confidenza al 95% per tutti i professionisti.

i ) Suppongo che il campione sia "grande" posso trovare una Z ~ N (0,1) tale che:

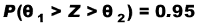
ii) Controllo le tavole (già sappiamo che θ1 = - 1,96 ; θ2 = 1,96)

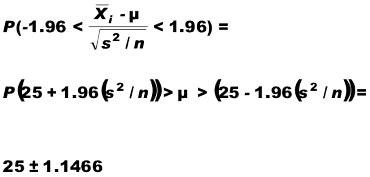
iii) Se il campione è piccolo, cosa succede?

Esercizio 3.6

Trovare ora la dimensione del campione che comporta un Intervallo di confidenza di 2$

TIRIAMO UN PO' DI SOMME!!!

Se σ fosse conosciuto potremmo "fare inferenza" sulla popolazione utilizzando le proprietà della distribuzione normale. Tuttavia, anche quando σè sconosciuto possiamo sostituirlo con la DS del campione s , a patto che si abbia a che fare con un campione "grande" . Cosa possiamo fare per campioni piccoli?

Problema quando il campione è piccolo e non si conosce σ

. Non possiamo utilizzare la distribuzione normale per formare IC

. Possiamo stimare il valore di σ dal campione

. Dobbiamo però usare la distribuzione t

La t è una FDP che presenta una forma è schiacciata rispetto alla Z

E' stata calcolata dal matematico inglese Gosset (1908), che la pubblicò sotto lo pseudonimo di Student

La sua forma esatta dipende dai gradi di libertà: GdL = n - parametri da stimare dove n è la dimensione del campione I valori della t sono tabulati (oppure si può usare la rete.)

Prof. Paolo Mattana

Successivo: Distribuzione t

Sommario: Index