La corretta specificazione del modello
- La specificazione del modello implica due ordini di scelte:
-->L'insieme delle variabili che vogliamo includere
--> La forma funzionale che vogliamo specificare
- Queste sono scelte che devono essere basate sulle teorie a disposizione
-"Can't get the right answer if we ask the wrong question"
- In generale, tutti I modelli sono "misspecified";
- Le teorie sono semplificazioni della realtà e tutte le misure sono imperfette;
- Ci accontentiamo di avere modelli "ragionevolmente" ben formulati (ed errori ragionevolmente modesti).
Si immagini che il modello vero possa essere rappresentato da:

Ma si stimi il modello:
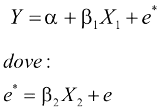
Conseguenze
- Il nostro modello viola l'assunzione E(e)=0

- Inoltre, cov(X1,e) diversa da zero
- Dunque, escludendo X 2 , rischiamo un coefficiente distorto per X 1
- Se il beta è distorto, anche s b lo è
Infatti:
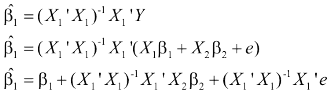
Se E(e)=0, allora la nostra stima di β 1 è:

- Questa relazione indica che la nostra stima di β 1è distorta per la presenza di 2 fattori distinti:
- L'entità della correlazione fra X 1 and X 2
- Il coefficiente di impatto di X 2 su Y (beta2)
- Spesso è difficile conoscere la direzione del bias
- Se entrambi questi fattori sono nulli, allora il bias è zero
- Si immagini un modello "vero" dove X 1 abbia un piccolo effetto su Y e dove esista una forte correlazione con X 2 che invece ha un forte impatto su Y.
- La specificazione di entrambe le variabili consente di separare gli effetti (si consideri il caso in cui non esista un rilevante effetto da multicollinarità
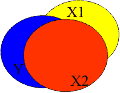
- Ma se stimiamo il modello semplificato (escludendo X 2 ), attribuiamo tutta la influenza causale a X 1
- Il coefficiente è troppo elevato e la varianza troppo bassa.

- Il problema è puramente teorico e non "statistico-econometrico"
- Non esistono test statistici che rivelano un errore di specificazione oppure OVB
-Si possono cercare altre X che sono potenziali fonti di OVB
- MOLTO MENO PROBLEMATICA
- Osserviamo lo stesso tipo di problemi se includiamo variabili irrilevanti?
- NO!
- Si immagini di stimare l'equazione:
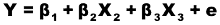
- Mentre il modello vero non contempla la X3
- Se β 3 = 0, la stima di β 2 non cambia
- Includere X non significative implica un maggiore s β2 2
- I MODELLI "VIRTUOSI" SONO QUELLI PARSIMONIOSI
Prof. Paolo Mattana
Successivo: Le dummies
Sommario: Index