Questo scenario crea complicazioni

- Y è già stocastica

- EM incrementa la componente stocastica di Y

- I coefficienti e le statistiche descrittive sono corretti

- Le stime sono meno efficienti

- La "Tolleranza" è un concetto complesso che è difficile misurare nelle interviste

-Tutta l'inferenza è corretta

- Tuttavia c'è più incertezza

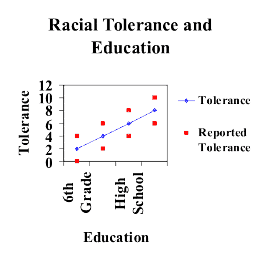
Modello stimato Y*=X β + e, dove Y*=Y+u

Errori di misurazione stocastici nelle variabili indipendenti

- Se X (stocastico) è misurato con errore, allora OLS è distorto

- Abbiamo correlazione simultanea tra X e termine di errore

- Ma cosa sappiamo riguardo la direzione del Bias?

- I coefficienti sono sempre sottostimati (mai sovrastimati)

- Dunque, i coefficienti possono essere non significativi a causa di EM

- Se però osserviamo un coefficiente "piccolo" malgrado la presenza di EM, sappiamo che il coefficiente vero sarà più grande in valore assoluto

- Di nuovo la "tolerance" è difficile da misurare, ma è ora una X e non una Y

- Cosa succede ora?

- Coefficienti non corretti

- Distorsione verso 0

- Perchè?

Perchè simultaneità? Si consideri il modello bivariato Y = α + ß X + e dove X (vero) è misurato con errore (X* = X + u) con E(u) = 0 e E(ue)=0.

Saremo costretti a stimare Y = α + ß X* + e - ßu = α + ß X* + ?

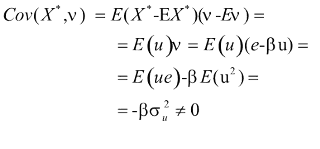
Direzione del bias dove X (vero) è misurato con errore (X* = X + u) con E(u) = 0 e E(ue)=0. Saremo costretti a stimare

Il coefficiente è distorto verso zero (sottostimato)

- Cosa fare in presenza di EM?

- Usare "IV" per eliminare la componente di errore dalle variabili

- Metodi di stima di equazioni simultanee

- Oppure tralasciare ogni eventuale correzione: in questo caso bisogna studiare bene le implicazione degli EM

Prof. Paolo Mattana

Successivo: Distorsioni da variabile omessa

Sommario: Index