Un raffinamento dell'analisi del MDD

Precedentemente si è mostrato come sia possibile simulare una distribuzione del MDD attraverso l'uso di un generatore di numeri casuali. La Figura 16 riporta un esempio ipotetico di una tale distribuzione. Si ricordi anche che tale distribuzione presuppone tra l'altrodi aver fissato un orizzonte temporale di trading. Un semplice raffinamento di quest'analisi permette di affrontare anche il problema dell'importo da investire.

Anzitutto si ricordi che la propensione al rischio è una materia ampiamente soggettiva, specialmente per quello che riguarda sistemi di supporto per la speculazione, e quindi non è possibile che esista un unico importo ottimo. E' peró possibile permettere all'analista di quantificare in qualche modo la sua propensione al rischio: ad esempio egli puó dire che gli risulterebbe inaccettabile perdere piú del 10% del capitale in un anno.

La Figura 17 mostra che - diciamo in un anno di trading - esiste il 5% di probabilità di perdere almeno 150 lire utilizzando il sistema a cui i dati si riferiscono [Si ricorda a costo di essere ripetitivi, che i dati in Figura 16 sono fittizi e non si riferiscono a nessun mercato in particolare.]Supponiamo altresí che tale risultato sia stato ottenuto da un sistema che metodicamente effettuava operazioni di importo nominale pari a 1000 lire.

E' importante osservare che nessuno puó garantire con assoluta certezza al nostro analista che egli non perderà piú del 10% del suo capitale in un anno. Come si è già osservato, i mercati presentano talvolta dei comportamenti totalmente inattesi ed entrambe la teoria finanziaria e l'esperienza indicano che non c'è ritorno senza rischio [Sia detto per inciso: se fosse possibile garantire al trader un rischio massimo (es. 10% del capitale in un anno) avremmo creato una strategia replicante un'opzione simile a quelle ottenibili con la cosiddetta "portfolio insurance". Ovviamente non è così e non è questo lo scopo che ci si è prefissi.

Strategie a rischio massimo garantito sono perfettamente raggiungibili ma l'esperienza ha più volte dimostrato che non hanno ritorni interessanti: si tratta perciò non soltanto di eliminare il rischio, ma di minimizzarlo.] L'analista puó peró decidere soggettivamente che il 5% di probabilità di perdere il 10% (o piú) del capitale è accettabile. In questo caso, una semplice moltiplicazione ci dice che per investire 1000 lire di capitale nominale nel sistema di trading in oggetto, l'analista dovrebbe averne da parte almeno 1500 (= 150 ??0.10 ?100). Questo capitale non necessariamente corrisponde al margine richiesto dal broker per effettuare le operazioni, anzi normalmente è sempre piú elevato. Si tratta piuttosto del capitale che si dovrebbe avere da parte per affrontare con la tranquillità desiderata il mercato con il sistema di trading oggetto dell'analisi. Questo capitale dovrebbe essere investito in attività senza rischio e dovrebbe generare (nella misura in cui non è utilizzato per far fronte al drawdown) un ritorno "risk-free".

Questo metodo di analisi puó quindi essere riassunto come segue.

	Si definisce un orizzonte temporale di trading (detto H) e si valuta il numero medio di operazioni che il sistema esegue in tale periodo di tempo.
	Si definisce una propensione al rischio in questo modo. Si sceglie anzitutto la percentuale R del proprio capitale che si è disposti a rischiare durante il periodo H. In secondo luogo si determina un livello P che rappresenta la probabilità di perdere R% del proprio capitale nel periodo H. Nè R, nè la probabilità P possono assumere valori nulli (cioè chi non risica non rosica).
	Si calcolano ripetutamente con il meccanismo descritto in precedenza le distribuzioni cumulate del MDD (ottenute dai dati di forward testing) per tutti i sistemi sotto analisi.
	Su tavole del tipo di quella riportata in Figura 16 si calcola per ogni sistema il capitale necessario. Il calcolo è effettuato moltiplicando il MDD corrispondente al P prescelto per la percentuale R per 100.

La simulazione qui effettuata attraverso un generatore di numeri casuali non equivale al lancio del "dado" ipotizzato nel paragrafo precedente a proposito dell'f ottimale. Anzitutto, la distribuzione dei risultati ottenuti in forward testing può qui essere ipotizzata come continua: è dunque possibile che vi siano operazioni simulate il cui risultato è diverso da quello di ogni operazione analizzata in forward testing.

In secondo luogo l'esperimento è ripetuto centinaia o migliaia di volte al fine di produrre sequenze di operazioni diverse. Quest'ultimo fatto, una sorta di analisi Monte Carlo semplificata, crea ipotetici periodi di trading che hanno un diverso numero di vincite e perdite, diversi importi di perdita massima e diversi MDD. Se si volessero calcolare gli f ottimali non se ne otterrebbe uno, bensì una distribuzione probabilmente composta da valori molto differenti e quindi con uno scarso valore operativo.

E' importante anche comprendere la relazione che esiste tra le tavole della distribuzione cumulata del MDD come quella di Figura 17 e la scelta dell'orizzonte temporale H. Nello schema proposto l'orizzonte temporale è effettivamente rappresentato dal numero medio di operazioni eseguite dal sistema su tale durata. Cosa succede se H viene ampiato, ad esempio se si passa da un anno a due anni? Succede che occorre raddoppiare anche il numero di estrazioni effettuate con il generatore di numeri casuali per ogni ciclo di trading. Così, se le operazioni erano 30 all'anno, ora saranno 60 per due anni.

Cosa succede alla distribuzione cumulata del MDD? La risposta a questo quesito è meno semplice di quello che sembra. Essa è equivalente alla risposta a questa domanda: "è piú rischioso investire in un certo sistema di trading per un anno o per due anni?". Tanto per cominciare occorre assumere che la distribuzione dei ritorni del sistema sia ugualmente stazionaria ad uno e a due anni, e questa è già una condizione difficilmente accettabile. Se si accetta questo, si puó ricalcolare la distribuzione dei MDD e si entra nel dominio di una delle piú sottili questioni della moderna teoria finanziaria e cioè se è possibile o meno trarre vantaggio da un effetto "diversificazione" temporale.

La trattazione di questo problema esce tuttavia dagli scopi di questo scritto ed il mio suggerimento all'analista è quello pragmatico di non dimenticare che l'unico orizzonte temporale ragionevole è quello per il quale si ritiene che la distribuzione dei ritorni (e quindi dei MDD) di cui si dispone sia significativa. E normalmente non si tratta mai di un periodo molto lungo [ Una semplice e breve introduzione al problema della diversificazione temporale la si trova in Kritzman (1994). In sostanza quest'autore afferma che non esiste un effetto diversificazione temporale nel caso che (1) i ritorni siano casuali e distribuiti log-normalmente, (2) l'avversione al rischio dell'investitore sia invariante a mutamenti della sua ricchezza, (3) la ricchezza futura dell'investitore dipenda solamente dai risultati dei suoi investimenti. Viceversa, se qualcuna di queste condizioni non è valida, come ad esempio nel caso di funzioni di utilità discontinu o ritorni non casuali, è talvolta possibile trarre un vantaggio dalla diversificazione temporale.

Una volta definiti l'orizzonte temporale e la propensione al rischio, è possibile dunque calcolare il capitale necessario per ciascuno dei sistemi di trading che sono stati testati. Tanto migliore è la distribuzione simulata del MDD, tanto minore è il capitale richiesto. Tuttavia questa è solo una parte della storia: sul mercato si va non solo cercando di minimizzare i rischi ma anche e soprattutto per guadagnare. A questo punto è peró
facile generalizzare l'analisi per ottenere anche una stima del ritorno del sistema. Vi sono due metodi.

Il primo metodo è "quick and dirty". Si conosce il numero di operazioni medie che si effettuano in H ed ovviamente si conosce anche (dal forward testing) il ritorno medio di una singola operazione. Infine si conosce il capitale necessario per poter affrontare il mercato con il sistema dato alle condizioni di rischio prefissate. Facile.

Esempio: H = 1 anno, 30 operazioni all'anno, rendimento medio di 5.5 lire per operazione, capitale richiesto alle condizioni di rischio prefissate di 1500 lire. Il ritorno percentuale annuo è di 11% ( = (5.5?30)/1500).

Il ritorno cosí calcolato si puó definire "aggiustato per il rischio" nel senso della definizione di rischio basata sul MDD che è stata qui presentata. Si tratta di un "excess return" in quanto ricordiamo che il capitale (o almeno gran parte di esso) dovrebbe già rendere un "risk free return".

Questo primo metodo sottintende tuttavia un'assunzione difficile da ingoiare. Si sta infatti accettando il fatto che il ritorno atteso sia sempre lo stesso qualunque sia il MDD. In realtà è altamente probabile che quando il sistema genera ampi valori di MDD, il ritorno finale sia ben inferiore a quello ottenibile quando il sistema genera un basso MDD. Anzi proprio la simulazione "tipo Monte Carlo" effettuata sul MDD permette senza sforzo anche il calcolo di una distribuzione di ritorni totali attesi lungo il periodo H. Conseguentemente è possibile associare ciascun ritorno ad una classe di MDD. Tutto questo puó essere visualizzato in un grafico come quello riportato in Figura 18.

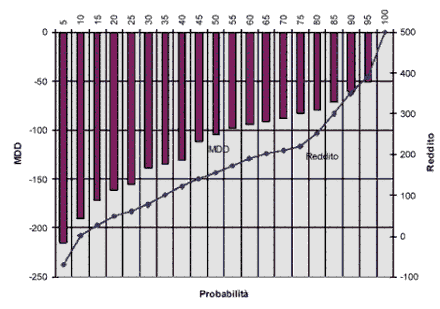
Figura 18: l' asse delle ascisse riporta la probabilità cumulata di ottenere un certo risultato (ad esempio c' è il 95% di probabilità di avere un reddito inferiore a 400), l' asse delle ordinate a sinistra riporta il MDD (rappresentato dalle barre) e a destra riporta il reddito (linea continua). I dati sono solo ipotetici.

Lo studio della figura non consente un calcolo numerico come quello realizzato con il primo metodo, ma permette un apprezzamento simultaneo delle condizioni di rischio e di ritorno, associate alle rispettive probabilità, del sistema in oggetto. Per concludere si puó dire che l'analisi del MDD si presenta come lo strumento piú flessibile e piú ricco di potenzialità per quanto riguarda l'analisi del rischio e della performance e quindi la validazione del sistema. Non è comunque inutile ricordare ancora una volta che essa è affidabile solo nella misura in cui la distribuzione dei ritorni ottenuta in forward testing puó essere ritenuta attendibile per il futuro.

[Sommario] [Successivo : Esempio. Parte III: calcolo dell'importo da investire ]