Nel XVIII° secolo, Newton (1642-1727) e Leibniz (1646-1716) dettero origine all'analisi ed al calcolo infinitesimale, elaborando le tecniche necessarie per derivare le funzioni. Apparvero funzioni discontinue o prive di tangente su un intervallo ovvero in un punto, ma queste funzioni erano considerate come eccezioni e l'attenzione era focalizzata sulle funzioni ben fatte. Matematici quali Gauss (1777-1855), Cauchy (1789-1857) e Dirichlet (1805-1859) ammettevano apertamente che una funzione continua di variabile reale fosse anche derivabile, salvo al più un insieme finito o numerabile di punti isolati. Con il 1870, ebbe inizio una crisi della durata di 50 anni che ha contribuito a trasformare le concezioni matematiche. Le funzioni tipo Weierstrass indicano quelle funzioni costruite da Bolzano (1781- 1848), Riemann (1826-1866), Weierstrass (1815-1897) ed altri, come contro esempi alla proprietà già citata sulla continuità e la derivabilità delle funzioni.E’ da notare che il procedimento costruttivo di Bolzano è geometrico ed è molto vicino a quello delle prime curve frattali, mentre l'esempio di Weierstrass è numerico. E’ opportuno anche ricordare l’esempio, di curva frattale fornito nel 1904 da Helge von Koch mediante una costruzione geometrica elementare: un esempio di curva continua e senza tangenti, Weierstrass sostiene che Riemann, in una comunicazione all'Accademia delle Scienze di Berlino nel 1872, avesse in mente un altro tipo di funzioni dal comportamento patologico. Egli aveva appreso da chi ne aveva seguito le

lezioni, che Riemann, nel 1861 o forse anche prima, aveva sostenuto che la funzione rappresentata dalla serie trigonometrica

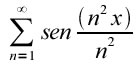
non verificava quella proprietà apertamente ammessa da matematici come Gauss, Cauchy e Dirichlet sulla non derivabilità delle funzioni di variabile reale continue. In merito alla funzione definita di Bolzano - Weierstrass, fu concepita da Bolzano allo scopo di dimostrare che la continuità non implica la derivabilità e che essa è non derivabile in nessun punto ma continua nell'intervallo [0,1]. Si consideri una successione di funzioni y1,y2,...yn...Il grafico di y1 è il segmento di retta congiungente i punti (0, 0) e (1, 1); il grafico di y2 è una linea spezzata che congiunge i punti (0, 0), (3/8, 5/8), (1/2, 1/2), (7/8, 9/8) e (1, 1); la curva y3 è ottenuta ripetendo l'operazione precedente su ogni segmento y2 e così di seguito. La successione yn ha per limite una funzione che non ha tangenti per nessun punto di [0, 1]. Per quanto questa sia soltanto una rapida presentazione dei principali contributi di Bolzano all'analisi matematica, si può evidenziare come abbia in realtà scoperto una funzione non derivabile in nessun punto ma continua in ogni punto in un intervallo dato.

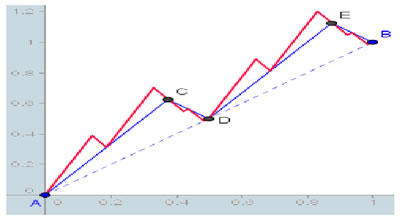
Illustrazione 6: Le curve a zig zag di Bolzano non derivabile in nessun punto ma continua nell'intervallo [0,1]

Successivo: 2.2.2.Von Kock, insieme di Julia, triangoli di Sierpinski

Sommario: Indice