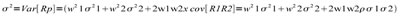Secondo l'approccio tradizionale in accordo con la Modern portfolio theory (MPT) di Markowitz, la teoria di portafoglio è espressa in funzione della domanda di attività finanziarie in funzione del loro rischio e rendimento data l'offerta di attività. La teoria nel dettaglio, cerca di far comprendere come mai gli investitori non àllochino l'intero risparmio in un'unica attività, distribuendo il patrimonio in più assets. E' un modello matematico che si basa in realtà su due uniche variabili, quali il rendimento atteso e la volatilità o varianza (deviazione standard d.s.) delle variabili casuali.

Misure del modello media varianza Il rendimento atteso e rischio di un titolo. Gli assunti fondamentali della teoria di portafoglio secondo Markowitz sono i seguenti: 1. Gli investitori intendono massimizzare la ricchezza finale e sono avversi al rischio.

2. Il periodo di investimento è unico. 3. I costi di transazione e le imposte sono nulli, le attività sono perfettamente divisibili. 4. Il valore atteso e la deviazione standard sono gli unici parametri che guidano la scelta. 5. Il mercato è perfettamente concorrenziale.

Il rendimento di un’attività finanziaria viene definito come il rapporto tra il capitale iniziale e gli utili prodotti da operazioni di investimento o di compravendita in un periodo di tempo specificato. Il rischio può essere definito come il grado di incertezza che il mercato esprime sulla effettiva realizzazione dei rendimenti attesi. Tanto il rendimento, quanto il rischio, possono essere oggetto di misurazione ex-ante ovvero sono ex-post. Il rendimento di un titolo azionario misurato ex-post su un periodo T, può essere espresso come:

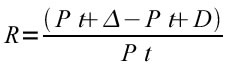
dove P(t) e

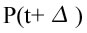
sono i prezzi di mercato negli istanti t e t+  e D il dividendo per azione riconosciuto dall’emittente. L’assunzione della della formula sopra trattata presuppone che il dividendo D, sia percepito all’istante T e che non sia reinvestito, che i costi di transazione siano nulli, che sia nulla la ritenuta fiscale sui dividendi e, infine, che T sia l’istante di valutazione.

Il rendimento ex-ante è quello stimato all’inizio del periodo di investimento T. Poiché per i titoli azionari le variabili

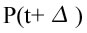
e D non sono note con certezza è necessario, per quantificare il rendimento atteso ex-ante, fare delle previsioni sul loro valore futuro. L’approccio classico considera R valutato ex-ante, come una variabile casuale caratterizzata da un valore medio (µ), che misura il rendimento atteso sul titolo, da un livello di varianza

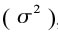
, assunto come misura attendibile dell’incertezza che venga perseguito quel livello di rendimento atteso e da una distribuzione di probabilità che identifica statisticamente il processo generatore dei prezzi.

In formula il rendimento atteso viene definito come:

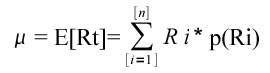
dove p(Ri) è la probabilità che il rendimento atteso, per il titolo i-esimo, sia Ri. La probabilità è definita come limite del rapporto tra il numero degli eventi favorevoli (Ni) e il numero totale di osservazioni (N):

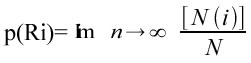
La formula sopra richiede, per essere calcolata, la stima di p (Ri) ottenibile dai modelli di analisi delle serie storiche o dall’analisi fondamentale. Avendo a disposizione un campione di N osservazioni sotto forma di serie storica dei rendimenti, si potrà dunque considerare la media aritmetica delle osservazioni come uno stimatore

attendibile del rendimento atteso µ. Il rendimento atteso è dunque in questa ipotesi definito dalla relazione:

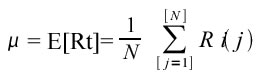
Nell’ambito della moderna teoria del portafoglio un’attività finanziaria si considera tanto più rischiosa quanto più elevata risulta la probabilità che i rendimenti futuri si disperdano rispetto al valore medio stimato. Una valida misura statistica di questo effetto è rappresentata dalla varianza, definita come somma degli scarti dalla media al quadrato pesati per le rispettive probabilità di realizzazione ed espressa dalla relazione:

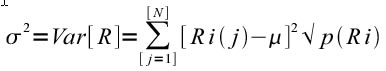
La funzione

assunta come una stima attendibile della rischiosità finanziaria del titolo, viene valutata mediante modelli matematico-statistici. Considerando la varianza campionaria come una stima attendibile della varianza dell’intera popolazione e indicato con N il numero di osservazioni delle quali si dispone, il rischio di un’attività finanziaria si calcola utilizzando la formula seguente:

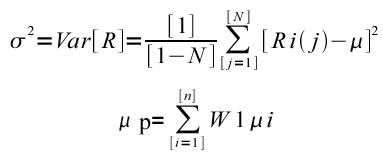
1N Un’assunzione fondamentale del mondo markowitziano, riguarda la distribuzione delle probabilità sulla quale si regge il meccanismo di formazione dei rendimenti, la quale si ipotizza essere di tipo Gaussiano. Ciò significa considerare che i prezzi siano generati da un processo casuale che esprime un valore medio atteso uguale a µ e una varianza pari a sigma 2 , assunzione assai utile dato che le variabili casuali distribuite normalmente sono descritte in modo completo dalle sole funzioni media e varianza. Per calcolare il rischio e il rendimento di un portafoglio costituito da N titoli è necessario fare riferimento alla correlazione esistente tra i titoli e al rapporto tra la frazione di ricchezza investita su ciascun titolo e quella totale di portafoglio Wj = Wj/ W. Si può dimostrare che per un portafoglio composto da n attività rischiose le espressioni del rendimento e della varianza ex-ante sono le seguenti:

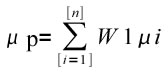
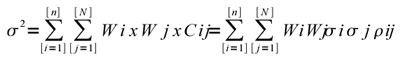
dove Wi è il rapporto tra la quantità di ricchezza investita sul titolo i-esimo e quella totale a disposizione dell’investitore, Cij e ij sono rispettivamente la covarianza e il coefficiente di correlazione tra il titolo i-esimo e il titolo j-esimo. E’ importante sottolineare che i rendimenti e le varianze attese per i singoli titoli che compongono il portafoglio sono considerate variabili casuali, governate da una distribuzione di probabilità condizionata che tiene conto del legame esistente tra un titolo e la rimanente parte del mercato. Nel caso di un portafoglio composto da due titoli si avrà:

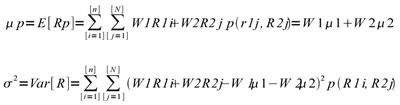
La formula precedente può essere riscritta come:

sostituendo alla funzione di covarianza la sua espressione in termini di coefficiente di correlazione lineare,

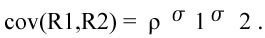
La formula ci dice che il rischio associato all’assunzione di un portafoglio composto da due titoli dipende anche dalla correlazione lineare esistente tra essi. Si riconosce che, se

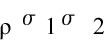
è nullo la varianza del portafoglio è uguale alla media ponderata delle varianze dei singoli titoli, pesate dalla percentuale di ricchezza in essi investita. In pratica se non c’è alcuna correlazione tra i due titoli il rischio di assunzione di un portafoglio è analogo a quello che caratterizza i singoli titoli. Se

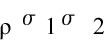
è positivo allora alla crescita del rendimento di un titolo corrisponde l’aumento del rendimento del secondo titolo, la variabilità del portafoglio, in questa situazione, è maggiore di quella che caratterizza ciascun titolo.

Se è negativo, il termine

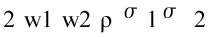
ha segno negativo e la varianza del portafoglio risulta minore di quella di ciascun titolo. Si deduce che nel caso di andamenti contrapposti dei rendimenti dei titoli, il rischio di detenzione di un portafoglio si riduce. Nell’ipotesi che tutta la ricchezza a disposizione sia investita nelle attività rischiose, è necessario aggiungere anche la condizione:

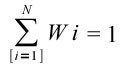
che definisce il vincolo nel processo di ottimizzazione del rapporto rendimento/rischio

Illustrazione 20: Frontiera efficiente con diversi indici di correlazione lineare

---

[42] Vedasi appunti del Prof. Carlo Bianchi e Prof. Davide Fiaschi di Note di Studio di Economia dei Mercati Finanziari Pisa 2009, nonché F.Orsi “Misurazione del rischio di Mercato” Pisa Plus 2009. II Edizione.

Successivo: 3.1 Multifractal Model of Asset Returns

Sommario: Indice