Il moto Browniano frazionario ed il suo processo incremento, il rumore gaussiano frazionario, sono spesso utilizzati per modellizzare fenomeni fisici che manifestano dipendenza a lungo raggio. Il moto Browniano fazionario introdotto per la prima volta da Kolmogorov e successivamente studiato da Mandelbrot e Van Ness, è un esempio di processo Gaussiano auto-similare ad incrementi stazionari con esponente di Hurst 0 < H < 1; Come si evidenzia nella Sezione 1 del lavoro, in un primo momento, l'impiego del moto Browniano, venne adottato nello studio di fenomeni fisici ed idrologici da parte ad esempio di Einstein per lo studio delle particelle in un liquido, evidenziando il movimento casuale di queste ultime nello spazio, movimento definito random walk o passeggiata casuale.

Partendo da questo concetto, Kolmogorov ed in seguito altri matematici, carpirono che non tutti i fenomeni naturali tracciassero percorsi casuali con un valore di H = 0,5 e che in natura, non potevano essere spiegati con una medesima legge, diversi eventi. Per acclarare la diversità dei valori naturali, i ricercatori passarono in rassegna diverse serie di dati, denotando che tra un periodo temporale recente, rispetto ad una sezione di una serie di dati remota, ci fosse una correlazione molto ampia che influenzava la tendenza della serie futura quasi prevedendone le mosse.

Partendo da questo presupposto, un idrologo britannico, Harold Edwin Hurst impegnato nei primi anni del 1900 in Egitto per determinare l'intensità delle piene del fiume Nilo, conseguì un risultato importante in base al quale le variazioni annuali del flusso del Nilo non fossero statisticamente indipendenti come nel modello di Bachelier48, ma che l'evoluzione dei fenomeni idrogeologici avessero una dipendenza positiva con quanto accaduto in passato e che i risultati delle ricerche effettuate divergessero non in funzione di un valore pari alla radice quadrata delle variazioni annuali del flusso, bensì di una potenza pari a 0,73.49 La sua formula50 iniziava calcolando le medie annue delle precipitazioni piovose, o della portata di un fiume, anno per anno, annotando le deviazioni cumulative, anno per anno da tale media.

Se, come nel caso di New York la piovosità media fosse di 106,5 cm annui, ma nel primo anno il valore effettivo fosse di 109, nel secondo 114, nel terzo 91 e nel quarto 112, allora le deviazioni cumulative sarebbero al primo anno 2,5,10 al secondo anno,-5,5 al terzo anno e 0 al quarto anno. Hurst considerò il valore massimo raggiunto dalle deviazioni cumulative pari a 10 in questo esempio e lo confrontò con il valore minimo -5,5. Chiamò tale differenza pari a 15,5 campo di variazione o range R. La sua formula fornisce il valore di R, che implica quanto dovrebbe essere grande un bacino di riserva per evitare inondazioni o siccità a valle. E' determinato dalla deviazione standard σ che rappresenta la variazione delle precipitazioni da un anno all'altro, da N, il numero di anni in esame e da α l'esponente della legge di potenza che regola l'intera equazione:

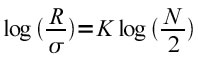
ovvero eliminando i logaritmi:

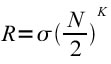
Mandelbrot, nel 1997, prendendo in considerazione il lavoro di Hurst ed applicatolo al caso del “cotone” ottenne un risultato nuovo secondo il quale una serie di dati presa in analisi fosse invariante rispetto al tempo e che tra le variabili rientranti nella serie

storica finanziaria, ci fosse una correlazione di lungo termine che con il decorrere del tempo riduce la sua intensità rispetto alla forza assunta in passato, ma che contribuirebbe comunque sul movimento dei prezzi della serie storica.

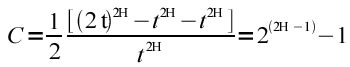
Si noti come C sia indipendente da W ed esprime la correlazione tra le variazioni della variabile in un certo intervallo temporale con le variazioni della stessa variabile in intervalli temporali della stessa lunghezza che seguono o precedono il primo51. Nel caso del coefficiente di Hurst = 0.5, siamo nel caso del Moto Browniano tradizionale o del modello Random Walk, la correlazione è C = 0 come sembra corretto affermare, visto che le variabili del modello sono i.i.d ovvero gli incrementi

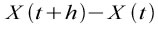
normalmente distribuiti saranno indipendenti rispetto al passato dimostrando che la loro distribuzione di probabilità sarà indipendente da t. Nel caso in cui invece il coefficiente Hurst assumerà valori

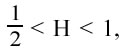
allora il valore della correlazione C sarà correttamente positivo, visto che il caso storico influenzerà il futuro e potremo affermare che gli incrementi non saranno indipendenti perché

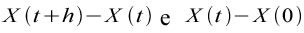
non avranno lo stesso segno a discapito di un valore di C negativo, nel caso in cui il coefficiente di Hurst sarà

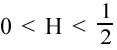
invece

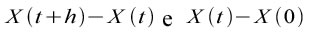
tenderanno ad assumere segni discordi. Questi fenomeni naturali seguono un andamento nel tempo che può essere descritto come un processo stocastico distorto noto anche come Moto Browniano Frazionario (FBM) e che in genere giustificano la presenza di una dipendenza di lungo periodo nelle osservazioni. Nel caso di

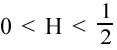
si dice che il Moto Browniano Frazionario è antipersistente Nel caso di

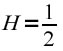
si dice che il Moto Browniano Frazionario è caotico

Nel caso di 0,5 < H < 1 si dice che il Moto Browniano Frazionario è persistente

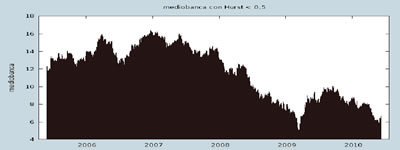
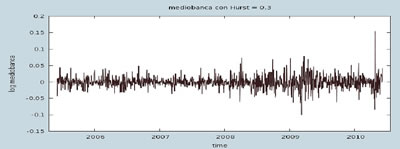
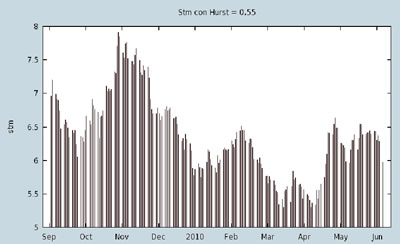
Illustrazione 24: Nei tre grafici sopra proposti sono esposti i casi dei diversi valori di Hurst

---

[48] La maggior parte degli ingegneri ed idrologici del XIX Secolo si servirono della tesi di Bachelier e della matematica classica per la realizzazione di progetti aventi ad oggetto la costruzione di dighe.

[49] Hurst, dopo i risultati conseguiti nel campo idraulico, pubblicò un lavoro dove racchiudeva la teoria secondo cui la Legge di Hurst (H Law) dimostrava che il campo di variazione dei livelli di piena cresceva in ragione della potenza di tre quarti della deviazione standard.

[50] H.E.Hurst, “Long-term storage capacity of reservoirs” in Transactions of the American Society of Civil Engineers ,1951

[51] C potrebbe esprimere la correlazione dei rendimenti ad un giorni dei prezzi di un titolo rispetto ai rendimenti , ad un giorno, rilevati in epoche passate e quelli che rileveranno in futuro

Successivo: 3.1.3 Il tempo di negoziazioni o trading time

Sommario: Indice