Attualizzazione dei dividendi, e tassi di crescita

Si è visto che i metodi di attualizzazione dei flussi di cassa consentono di generare una stima del prezzo come valore attuale di entrate future. Sebbene come è logico le entrate di un’impresa sono rappresentate dagli utili, non si può scontare direttamente questa grandezza per giungere ad una stima del prezzo. Il prezzo deve riflettere il valore attuale dei flussi che arriveranno effettivamente nelle tasche dell’ azionista, e perciò il valore dei futuri dividendi, visto che la distribuzione degli utili sotto questa forma è del tutto discrezionale.

Molte imprese, soprattutto quelle più grandi e con partecipazioni pubbliche, spesso adottano una politica di distribuzione di dividendi indipendentemente dal risultato economico, ed in questi casi è indubbiamente molto più agevole la stima del valore attuale. Nel suo manuale di valutazione finanziaria, il professor Aswath Damodaran[58] suggerisce di prestare attenzione, nell’ambito di questo modello, oltre che ai dividendi anche al tasso di crescita degli utili e alla componente rischio, in quanto queste sembrano essere le leve discrezionali più influenti.

Effettivamente gli stessi titoli, valutati con il Dividend Discount Model, possono condurre a stime molto diverse se si scelgono tassi di crescita o rischio implicito anche di poco differenti.

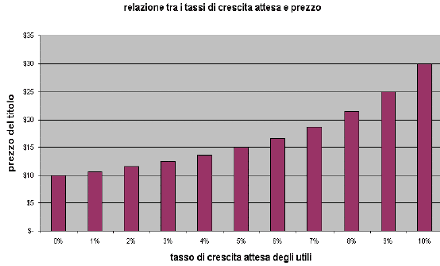
Figura 12. Relazione tra i tassi di crescita attesi e il valore di un titolo.

Nella Figura 12, si è preso in considerazione un titolo che paga un dividendo di 1,5$, un tasso di sconto (il rendimento atteso del capitale comprensivo del rischio) del 15% e si è evidenziata la diversa valutazione del prezzo del titolo sulla base della scelta di differenti tassi di crescita attesi degli utili. In particolare si vede passare il prezzo da 10$ a 30$ al variare del tasso di crescita da 0 al 10%. La formula utilizzata in questo è la seguente:

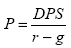(7.1.4)

Questa versione del modello di attualizzazione dei dividendi (Dividend Per Share è la sigla utilizzata nella formula) è molto semplice in quanto riconducibile alla formuna di una rendita perpetua. Al denominatore al posto del semplice tasso di sconto compare la differenza tra due tassi. Il secondo di questi è proprio il tasso di crescita degli utili, growth rate, che riducendo il denominatore fa crescere ovviamente la stima del prezzo. Questa variante del modello di attualizzazione è conosciuta come modello di Gordon.

Naturalmente ciò che rende poco verosimile una soluzione così semplice è il fatto che parametri come i dividendi, o il tasso di crescita stimato, non possono essere ritenuti costanti per lunghi periodi, e sebbene l’utilizzo di una rendita perpetua dia immediatamente l’idea di quali prospettive offrirebbe un titolo se le condizioni si prolungassero indefinitamente nel tempo, nell’analisi finanziaria le valutazioni devono tenere conto di innumerevoli fattori, come la ciclicità dell’economia, le diverse fasi di sviluppo di un business, la rischiosità del settore, la qualità dei dati disponibili, etc.

Per costruire un modello di attualizzazione dei dividendi, prima di tutto occorre avere a disposizione una stima dei dividendi stessi attesi. Per ottenere questo si parte dallo studio di dati passati relativi agli EPS (Earning Per Share) dai quali in base alle politiche di payout seguite nei singoli casi si possono estrapolare i dati relativi ai dividendi. Il modo più naturale di fare previsioni sugli utili futuri partendo dai dati passati è quello di ricorrere a modelli di regressione lineare o logaritmica, che danno luogo ad una formulazione del tipo EPSt = a + bt, in cui il coefficiente angolare della variabile temporale, esprime la variazione degli utili nel tempo.

La versione logaritmica consente di rendere tale coefficiente un termine percentuale. Previsioni migliori possono essere ottenuti con un più specifico esame delle serie storiche, e di questi strumenti, come le medie mobili integrate autoregressive (modelli ARIMA) si tratterà specificamente nel capitolo seguente. Una volta ottenuta una soddisfacente stima dei dividendi attesi, si deve cercare un appropriato tasso di crescita da inserire nella formula.

In finanza aziendale quando si parla di crescita, si fa riferimento all’equazione della crescita sostenibile, nella quale si considerano il tasso di ritenzione degli utili (dunque crescita dovuta dall’autofinanziamento tramite il reinvestimento degli utili nell’attività di impresa), il rendimento del capitale investito dopo le tasse e prima degli oneri finanziari (il ROA) e il grado di leva finanziaria (ovvero il rapporto tra il BV dell’ammontare di indebitamente ed il BV dei mezzi propri). L’espressione caratteristica è la seguente:

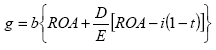(7.1.5)

A questo punto è possibile introdurre un modello di sconto dei dividendi completo, ovvero che sia costruito tenendo presente la dinamica più reale possibile legata alla crescita di un’impresa. Tale crescita infatti subisce verosimilmente un cambiamento nelle diverse fasi di sviluppo di un determinato business. Si può supporre che all’inizio dell’attività di un’azienda venga sostenuto un tasso di crescita elevato dovuto alla diffusione di una certa tecnologia, di un prodotto o di un servizio. Successivamente, nella fase di stabilizzazione il tasso di crescita diminuirà gradualmente fino a posizionarsi ad un determinato livello.

A questo punto si suppone che a tempo indeterminato la crescita rimanga costante. Al contrario i payout ratio seguiranno una evoluzione opposta crescendo in modo proporzionale al grado di affermazione conquistata dall’impresa. Damodaran propone un modello a tre stadi in cui si presuppone una fase di crescita elevata, una fase di crescita decrescente ed una fase di crescita stabile all’infinito[59]. Il prezzo di conseguenza risulta dal valore attuale dei dividendi dei tre diversi stadi:

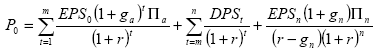(7.1.6)

in cui g_a e g_n sono rispettivamentei tassi di crescita nella fase iniziale e nella fase di stabilizzazione, mentre a Π e n Π sono i due diversi tassi di distribuzione degli utili nelle due rispettive fasi di crescita. Il modello presuppone che il tasso di crescita decresca linearmente e che altrettanto linearmente aumenti il tasso di distribuzione tra la prima e la terza fase.

In sintesi il metodo dei flussi di cassaè un metodo che offre delle valutazioni molto significative, a patto di riuscire attraverso l’informazione disponibile a manovrare tutte le leve che questi modelli incorporano. Le difficoltà in questo senso possono derivare dalla presenza di flussi di cassa non stabilmente positivi, o poco affidabili, ovvero in assenza di una corretta stima del rischio da associare al tasso di sconto.

Esempi di difficoltà di utilizzo di tale metodo sono le aziende cicliche, o in crisi, in cui la discontinuità o la negatività dei flussi comporta non pochi problemi. A tal fine risulta produttivo ricorrere anche ad altri parametri di valutazione quali i multipli.

58 Si veda Damodaran, A. Manuale di ValutazioneFinanziaria (1996).

59 Si veda Damodaran, A. Manuale di Valutasione Finanziaria, 1996. pag. 130.

Marco Primavera

Successivo: Metodo dei multipli

Sommario: Index