Res Tantum Valet quantum vendi potest

Nel capitolo precedente si sono elencati i principali argomenti concernenti la teoria del mercato efficiente, e nel capitolo 9 verranno esaminate più in dettaglio le singole anomalie ed i casi che evidenziano una mancanza di efficienza. In questo capitolo invece si cercherà di porre un po’ di chiarezza sul ruolo di tutte queste teorie contrastanti e spiegare in che modo giustificano le bolle speculative.

Ciò che sta alla base di tutta la ricerca in questo campo è il tentativo di dare un senso ai fenomeni di persistente deviazione dei prezzi da un valore razionale, ovvero riconducibile a dati fondamentali. In realtà il concetto di razionalità non è così direttamente legato a quello di dato fondamentale, bensì include tutta una serie di circostanze informative, emozionali e speculative che pur non potendo essere lette all’interno di un quadro fondamentale, producono spesso l’ effetto alterare i prezzi in modo apparentemente esagerato.

La bolla speculativa consiste dunque in una divergenza dei prezzi protratta per periodi lunghi, e quindi difficile da conciliare con la EMH, eppure anche questi fenomeni trovano una spiegazione secondo i sostenitori del mercato efficiente. Ad esempio si è visto nella parte relativa alla rassegna storica come i bulbi di tulipano avessero raggiunto prezzi incredibili, ma questi prezzi si riferivano a bulbi con delle particolari colorazioni (che in realtà per alcune specie erano semplicemente dovute ad una malattia) ed effettivamente molto rari, perciò il fatto che taluni “estimatori” fossero disposti a pagarli molto, secondo alcuni potrebbe non essere un segnale di irrazionalità.

Jeremy Siegel, nel suo celebre Stocks for the Long Run, spiega che in cinquanta titoli soprannominati Nifty Fifty nei primi anni ’70 non erano sopravvalutati come si fece notare nel ’77, dopo che questi avevano perso parte del loro valore, in quanto nel lungo periodo avrebbero garantito in media la stessa performance dello S&P500[52]. Sulla formalizzazione delle bolle si sono concentrati diversi modelli matematici tentando di definire le caratteristiche principali di questi fenomeni, e prima ancora, tentando di verificarne la possibile esistenza.

Tutta la modellistica sulle bolle razionali, in sostanza cerca di rendere plausibile una struttura del prezzo, percepito con aspettative razionali, composto da una componente fondamentale e da una componente bolla, la quale dovrebbe essere parimenti scontata nel valore attuale di un’azione e che risponde secondo le diverse teorie a determinate caratteristiche. A cominciare dai primi anni ’80, molti studiosi come Blanchard e Watson (1982), Flood e Garber (1980) o Hamilton e Whiteman (1983) si sono dedicati alla spiegazione delle bolle in termini il più possibile compatibili con la teoria dell’ efficienza, che da Fama in poi ha riscosso sempre più credito.

Lo studio delle “bolle razionali” è allacciato alla teoria delle aspettative razionali, ampiamente utilizzata nei modelli di economia monetaria. Infatti la formalizzazione matematica della bolla si può far risalire al modello di iperinflazione di Cagan (1956) esteso alle RE (Rational Expectations):

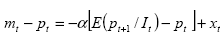(6.1)

dove mt e pt sono i logaritmi naturali della quantità di moneta e dei prezzi; 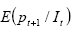esprime l’aspettativa razionale riguardo p_t+1 sulla base del set di informazione disponibile I_t . x_t è la componente di disturbo. Assumendo mt come determinata esogenamente ed α >0 l’equazione può essere riscritta nella sua forma più consueta:

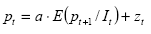(6.2)

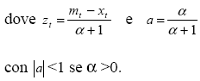
In questo modo si esprime una variabile endogena come una funzione lineare del suo valore atteso per il periodo successivo, e di un termine esogeno zt . Tale formulazione ricorre in molti modelli sulle bolle razionali, e dal momento che questa equazione ha infinite soluzioni, si deve prestare attenzione alla cosiddetta “forward-solution”, o soluzione fondamentale, ricavata per sostituzioni ricorsive (Blanchard, 1979).

(6.3)

in cui si esprime pt in funzione del valore atteso di variabili esogene del sistema. La serie non è necessariamente convergente, e la forward-solution non esiste necessariamente, a meno che il processo zt non sia stazionario e . Purtroppo non è possibile fare in modo, nella maggior parte dei modelli, che pt sia espressione esclusivamente dei fondamentali dell’equazione qui sopra.

E sulla base di questa debolezza si fondano teorie sulle bolle razionali che vedono le deviazione del prezzo dai fondamentali non necessariamente come una prova evidente di irrazionalità. Le aspettative razionali possono infatti andare d’accordo con le self-fulfilling expectations e gli altri fenomeni della psicologia di massa che sono stati esaminati nella seconda parte del presente lavoro. Per formalizzare tale versione di una bolla si parte dalla soluzione fornita da Gourièroux, Laffont e Monfort (1982)

(6.4)

in cui Nt è una martingala arbitraria, ovvero un processo in cui l’aspettativa razionale del valore x_t coincide con x_t-1 . In generale le martingale includono componenti stocastici a media zero, tali da renderli del tipo

(6.5)

in cui il processo stocastico è rappresentato da θt.

La soluzione pt può essere di conseguenza scritta come

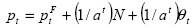(6.6)

da qui si può estrarre la componente bolla come differenza tra ciascuna soluzione ed il valore fondamentale p_t^F :

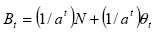(6.7)

dove Blanchard e Watson (1982) specificano che il primo termine coincide con la componente deterministica della bolla, ed il secondo termine ne esprime la componente stocastica. Ovviamente la componente più interessante e malleabile è proprio quest’ultima, in quanto può essere resa espressione di informazione ed altre variabili imprevedibili in grado di influenzare la soluzione.

Tuttavia essendo riconducibile alla componente deterministica l’elemento “self-fulfilling” delle aspettative, si deve tenere conto della possibilità di riconoscere entrambe le componenti, anche se di solito si studiano separatamente. Perché un modello sia realistico necessita dell’introduzione di dinamiche più complesse con valori ritardati delle variabili endogene o con aspettative di diverso orizzonte. Ma neanche in questo modo sarebbe possibile risolvere il modello con sostituzioni ricorsive, e non ci sarebbe comunque coincidenza tra i fondamentali e la forward-solution.

Inoltre si ricorda che nel modello di iperinflazione visto all’ inizio si da per scontato che tutti gli operatori siano a conoscenza del meccanismo di formazione dei prezzi e che la struttura informativa sia omogenea, nel senso che tutti gli operatori fanno riferimanto allo stesso set di informazioni It . Ovviamente laddove tali presupposti non fossero rispettati cambierebbe il processo di formazione delle aspettative e quindi la determinazione della bolla. Diba e Grossman (1986) si sono concentrati sulla fase di inizio di una bolla razionale[53].

Una bolla che comincia dopo il primo giorno di trading ha un valore atteso pari a zero, e visto che la possibilità di vendere rende impossibile il verificarsi di bolle razionali negative (dal momento che gli azionisti non possono aspettarsi che il valore di un’azione decresca illimitatamente), questo valore atteso iniziale può essere pari a zero soltanto se sono uguali a zero (con probabilità unitaria) tutte le possibili realizzazioni di bolle razionali. Questo significa che l’impossibilità di verificarsi di una bolla razionale negativa rende impossibile anche l’inizio di bolle positive, se non dal primo giorno di contrattazione del titolo, e questo di per sé è incompatibile anche con il modello empirico di Blanchard in cui era possibile che le bolle razionali si gonfino, scoppino e ricominciano a gonfiarsi successivamente.

L’articolo di Diba e Grossman, muove dallo sviluppo delle proprietà formali di una bolla razionale, ottenute a partire dalla massimizzazione di una funzione di utilità, per poi derivare la condizione che se una bolla razionale esiste deve essere iniziata con il primo giorno di contrattazioni dell’attività. Successivamente dimostra che tale bolla non può scoppiare e conseguentemente tornare a gonfiarsi. Infine propone l’ipotesi di orizzonti di pianificazione finiti per analizzare le conseguenze diverse riscontrabili nella bolla.

---

52 Si veda Siegel, J. Stock for the Long Run (1998).

53 Si veda Diba, Behzad, T., Grossman, Herschel, I. On The Inception of Rational Bubbles In Stock Prices. NBER, 1986.

Marco Primavera

Successivo: Bolle Razionali II

Sommario: Index