L’analisi di cointegrazione

Con questo tipo di analisi è possibile stabilire un legame lineare stazionario tra processi stocastici non stazionari, di modo da individuare una relazione stabile nel tempo tra variabili che prese singolarmente non sono stabili. In particolare si parla di serie integrate di un certo ordine p, in cui p rappresenta il numero di differenze necessarie a rendere stazionaria una serie.

In genere in tema di cointegrazione si ha a che fare con serie I(1), in cui ciascuna variabile è integrata di ordine 1, quindi tale che la differenza prima della variabile è di tipo I(0), ovvero stazionaria. Si noti che in economia non si osservano di solito variabili integrate di ordine superiore ad 1. La nozione di cointegrazione emerse dal dibattito circa le regressioni spurie nelle serie storiche. Una relazione di variabili economiche del tipo 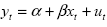produce spesso risultati empirici in cui il coefficiente di determinazione R² è abbastanza alto, ma la statistica Durbin-Watson è bassa.

Questo accade perché le serie economiche presentano un trend di lungo periodo. In pratica le singole variabili, come si era accennato poco fa, si comportano come random walks non stazionarie. Anche se è possibile combinare due variabili di questo tipo in un modello in cui 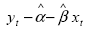appare stazionario, questo risultato è comunque poco utile nelle relazioni a breve termine tra y_t e x_t. Se infatti entrambe le serie sono integrate di ordine 1, si dovrà spesso rifiutare l' ipotesi di assenza di relazione anche quando non ce n' è alcuna.

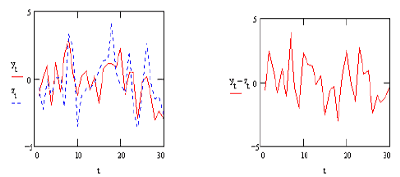Figura 21. Fonte: sito internet del prof. A.J. Buck, Temple University

I due processi disegnati nel riquadro a sinistra della figura 21 sono entrambi dei White Noise, che hanno la stessa deriva (drift), e pertanto sono stati cointegrati in modo da rendere stazionario y_t - z_t.[65]

65 Per ulteriori analisi sulla cointegrazione si veda il sito internet del Prof. Buck http://oll.temple.edu/economics/notes/lectures_rev.html

Marco Primavera

Successivo: EMH: L'evidenza del contrario

Sommario: Index