L’ipotesi di stazionarietà

Nelle analisi delle serie storiche il problema più rilevante è la dipendenza dei processi, o per meglio dire dei momenti del processo dalla variabile tempo. Questo significa che il valore atteso, come pure la varianza del processo stocastico analizzato è posto in una condizione di perenne mutabilità proprio perché funzione di una variabile che non assume mai, per definizione, lo stesso valore, ovvero t.

Tutti i momenti del processo, compresi quello importante dell’autocovarianza e la funzione di autocorrelazione, sono direttamente legati al problema della variabile tempo. Per questo si fa spesso riferimento ad un’ipotesi di comodo, la stazionarietà, che permette di leggere un processo estrapolandolo dalla dimensione temporale.

La definizione di stazionarietà si divide in due forme, debole e forte, di cui la seconda talmente restrittiva e poco riscontrabile, che non verrà menzionata. Nell’accezione che qui interessa, (la forma debole) definiamo stazionario quel processo stocastico che rispetti le seguenti condizioni:

(8.3.1)

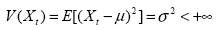(8.3.2)

(8.3.3)

Con µ, σ² e γ(k) indipendenti dal tempo; σ² con un valore finito; γ(k) dipendente solo da K. Un esempio di processo stazionario è il White Noise (WN), nel quale le variabili casuali hanno una distribuzione indipendente ed egualmente distribuita. Una delle conseguenze più interessanti di questa differenza tra serie stazionarie e non, si riscontra in presenza di uno shock.

Mentre per le serie stazionarie qualunque shock è destinato ad essere riassorbito al tornare della serie verso la media di lungo periodo, ciò non accade nelle serie non stazionarie. Infatti essendo i momenti di questo processo legati alla variabile tempo, da una parte non esisterà una media di lungo periodo, dall’altra la varianza tenderà ad infinito come il tempo, di cui è funzione.

Oltretutto il correlogramma di una serie non stazionaria non è decrescente come quelli delle serie stazionarie: al massimo risulterà, per campioni finiti, decrescente in modo molto lento. Questo ovviamente rende difficile rilevare la presenza di un trend.

Marco Primavera