Sebbene i modelli stocastici di bolle speculative visti precedentemente, come quello di Blanchard e Watson (1982) consentono delle deviazioni persistenti tra il prezzo di mercato ed i fondamentali a prescindere dallo studio della correlazione seriale, tali tipi di bolle non sembrano compatibili con i limiti e gli errori di valutazione commessi dagli speculatori e con le reali opportunità di investimento.

Il presente paragrafo si propone di studiare il fenomeno della mean reversion, intesa come la tendenza dei prezzi azionari ad essere “attratti” verso il loro valore medio di lungo periodo, presentando un comportamento in disaccordo, ancora una volta con la teoria dell’efficienza. In pratica, per alcuni asset, nonché per i tassi di interesse e forse anche i tassi di cambio, sembra che il moto geometrico Browniano (GBM), anche conosciuto come processo di Wiener, cui si fa riferimento come modello di processo stocastico rappresentativo di andamenti soggetti a molteplici shock, sia sostituibile con un modello “mean-reverting”. Per evidenziare la differenza si deve supporre una forma del tipo:

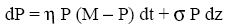(9.7.1)

in cui η è la velocità del processo di reversione ed M è il prezzo medio di lungo periodo verso cui avviene la reversione, mentre gli altri termini rimangono gli stessi di un normale GBM[87]. La differenza tra un processo di mean reversion ed il moto Browniano è semplicemente nel termine di deriva: infatti il Drift Term è positivo se il livello di prezzo corrente è inferiore alla media e negativa se il livello di prezzo è superiore, indicando appunto che tale livello di equilibrio attrae verso di sé la deriva.

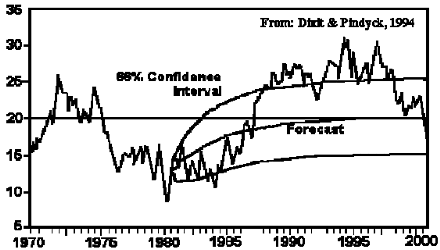
Figura 25. Intervallo di confidenza nella previsione del processo di mean reversion.

Nella figura 25, tratta dal libro di Dixit e Pindyck è disegnato il processo in questione, con un intervallo di confidenza del 66% relativo alla previsione dell’andamento successivo ad un punto in cui il tracciato è situato sotto la media di riferimento. La mean reversion è un processo a diffusione lognormale, ma con una varianza che cresce non proporzionalmente all’intervallo di tempo, infatti cresce all’inizio e si stabilizza successivamente su un determinato valore.

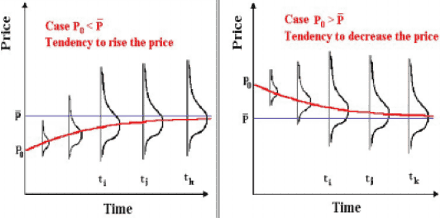
Figura 26. Direzione della deriva nel processo di mean reversion.

Il primo articolo significativo che documentasse questo fenomeno è stato quello di James Poterba e Lawrence Summers (1988) i quali partendo dall’analisi della varianza dei rendimenti per gli Stati Uniti ed altri 17 paesi sono giunti alla conclusione che sebbene a livelli statistici convenzionali non possa essere rigettata l’ipotesi random walk, è riscontrabile una correlazione negativa nei rendimenti per periodi superiori ad un anno, ed una correlazione positiva per periodi brevi (una settimana, un mese).

Per capire cosa significhi questo si deve tornare al Variance Ratio, visto poc’anzi. Tale test è motivato dalla nozione che se i dati sottostanti che generano il processo relativo ai rendimenti azionari sono serialmente random con varianza costante, allora la varianza dei rendimenti per K periodi è semplicemente Kσ² , dove σ² è la varianza del rendimento di un periodo[88]. Dunque la versione più semplice del VR è:

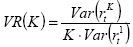(9.7.2)

dove r^K_t è il rendimento del periodo K.

Per rigettare l’ipotesi nulla di random walk tale rapporto, come si è detto, deve essere significativamente diverso da 1. Cochrane (1988) osserva che tale ratio può essere approssimato da:

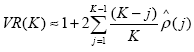(9.7.3)

dove ^ρ(j) denota il coefficiente di autocorrelazione del campione, di ordine j, relativamente al rendimento azionario di un periodo. In questa forma si può evidenziare la relazione tra VR e l’autocorrelazione campionaria dei rendimenti di un periodo. In ultimo per tenere conto della presenza di distorsioni transitorie dei prezzi in grado di abbassare il rapporto sotto l’unità, si divide per il valore atteso del variance ratio E[VR(K)], ottenendo la combinazione lineare di autocorrelazioni utilizzata da Poterba e Summers[89]:

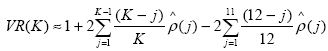(9.7.4)

adattata per tenere conto della varianza dei rendimenti mensili. Nell’analisi dei rendimenti reali ed in eccesso i due studiosi hanno preso come riferimento il tasso privo di rischio dei Treasury Bill ed il Consumer Price Index (CPI) ed hanno proceduto a studiare i rendimenti mensili (sia i Value-Weighted che gli Equal-Weighted returns) del NYSE per il periodo 1926-1985. I risultati di Poterba e Summers, confemano quelli ottenuti da Fama e French (1988b), secondo cui sia i rendimenti reali che quelli in eccesso mostrano per orizzonti lunghi una correlazione seriale negativa.

In particolare i coefficienti di regressione multi-periodali danno luogo ad un andamento a forma di “U” all’aumentare del numero di periodi N: per piccoli valori di N le correlazioni sono prossime a zero; raggiungono un minimo dopo 3-5 anni e poi tornano verso zero. La mean reversion è più evidente per i rendimenti ugualmente ponderati che per quelli indicizzati, ma il VR per orizzonti lunghi è decisamente inferiore all’unità per entrambi. In compenso la varianza dei rendimenti relativi ad un mese su indice equiponderato è solo il 79% della varianza che implicherebbero i rendimenti su 12 mesi. Lo stesso accade per l’indice Value Weighted e questo è in linea anche con l’analisi di Lo e MacKinlay (1988) secondo la quale il VR eccede l’unità nei dati settimanali e cade al di sotto dell’unità per orizzonti più lunghi[90].

Le applicazioni del Markov-Switching Variance Model da parte di Kim, Morley e Nelson (2000) suggeriscono che soprattutto per holding periods di 72 e 96 mesi, segnali più forti di mean revesion coincidono con “dramatic shifts” nella volatilità del mercato, ma che questo fenomeno d’altra parte, come era stato già argomentato in un articolo precedente (Kim, Nelson, Startz, 1991) troverebbe riscontro solo nel mercato degli anni precedenti la seconda guerra mondiale. Ancora questi tre autori, in un articolo del 2001 propongono di spiegare il comportamenti “mean reverting” delle attività finanziarie con un tradeoff intertemporale tra rischio e rendimento, partendo dal presupposto che esista una forte relazione positiva tra la volatilità del mercato ed il rendimento atteso[91].

Ma Kent Daniel preme a puntualizzare, in un suo articolo[92], che i test che si fanno sulla mean reversion sono spesso deboli e non riescono a rilevarla. In particolare Daniel ha preso in considerazione test di autocorrelazione ponderata, test di regressione su lunghi orizzonti, variance ratio, test spettrali ponderati e metodo generalizzato dei momenti applicato a funzioni dei rendimenti passati, e successivamente attraverso il calcolo della distribuzione della statistica-T di Fama e French corretta per piccoli campioni rileva una forte evidenza di mean reversion.

In Econometrics of Financial Markets, Campbell, Lo e MacKinlay affermano che la debole presenza di mean reversion nell’orizzonte di lungo periodo “è un sintomo della misura ridotta del campione, ancorché un’evidenza conclusiva contraria al fenomeno”[93]. Sembra dunque che il problema nella rilevazione di mean reversion sia la mancanza di serie storiche lunghe ed attendibili, anche perché si presume che questo comportamento si manifesti con una certa lentezza e perciò per essere catturato necessita di intervalli significativi. Oltretutto come notano Fama e French (1988) c’è il problema dell’identificazione di un “trend path” cui far riferimento, e di fatto operando una differenziazione di primo ordine della serie storica, come hanno fatto questi due studiosi, si perde dell’informazione utile ad identificare un eventuale comportamento mean reverting.

Nel loro articolo, Balvers, Wu e Gilliland (2000) studiano gli indici azionari di 18 paesi disponibili nel Morgan Stanley Capital International (MSCI), per il periodo 1969-1996. Partendo dall’assunzione che la differenza tra il trend-path dell’indice azionario di un paese e quello di un indice di riferimento sia stazionaria e che la velocità della reversion nei diversi paesi sia simile, la mean reversion può essere rilevata relativamente ad un indice di riferimento evitando il problema di identificare un trend-path.

Nell’articolo in questione oltre a rigettare l’ipotesi di assenza di mean reversion se ne individua una “half-life” dai 3 ai 4,5 anni. Miller, Muthuswami e Whaley (1994) affrontano anche il tema dibattuto della mean reversion intraday, ma giungono alla conclusione che si tratti di una normale conseguenza dell’index arbitrage e dell’infrequent trading, mentre si mostrano più incerti nell’affermare se la prevedibilità intraday sia o meno un’illusione statistica.

---

87 Tale formulazione è quella presente in Dixit Avinash, k. e Pindyck Robert, S. Investment under Uncertainty, Princeton. 1994.

88 Si veda Kim, M.J., and Nelson, C.R., and Startz, R. Mean Reversion In Stock Price? A Reappraisal of Empirical Evidence. The Review of Economic Stidies, 1991.

89 Poterba, L., and L. Summers. Mean Reversion In Stock Prices: Evidence and Implications. Journal of Financal Economics, 1988.

90 Si veda anche French e Roll (1986).

91 Si veda Kim, Chang-Jin, and Morley, James C., and Nelson Charles R. Does an intertemporal tradeoff between risk and return explain mean reversion in stock prices?, Maggio 2001.

92 Si veda Daniel, K. The Power and Size of Mean Reversion Tests, Forthcoming in the Journal of Empirical Finace, 2001.

93 Campbell, John Y., Andrew Lo, Craig Mackinlay. The Econometrics of Financial Markets. Princeton (1997), pag 80.

Marco Primavera

Successivo: Riscontri dall'analisi "Level AR"

Sommario: Index