Bolle Razionali II

A differenza del modello di Blanchard e Watson (1982), in cui i detentori di equity ricevono un tasso di rendimento costante, Quah (1985) propone un modello in cui il prodotto del prezzo di un’azione per l’utilità marginale del consumo soddisfano un’equazione differenziale lineare di primo grado sulle aspettative, che ha un autovalore maggiore dell’unità ed un termine stocastico che riflette l’evoluzione attesa dei dividendi dell’azione.

Grossman e Diba fanno riferimento ad una soluzione particolare di questa equazione differenziale, riferita alla componente fondamentale del prezzo dell’azione, che eguaglia il prezzo al valore attuale dei dividendi scontati al tasso marginale di sostituzione intertemporale atteso. Tale fattore di sconto dipende unicamente dal processo che genera benefici e dividendi, e dal tasso di preferenza temporale, entrambi i quali sono determinati esogenamente. La soluzione generale a tale equazione permette di dividere il prezzo dell’azione in una componente fondamentale ed in una componente di bolla razionale.

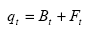(6.8)

in cui Bt è la soluzione alla seguente equazione:

(6.9)

come si vede qualunque valore di Bt diverso da zero presuppone già al tempo t l’esistenza di una bolla e quindi l’aspettativa auto-confermante che che qt non dipende solo da Ft . L’ipotesi di aspettative razionali fa dunque sì che nella mente degli azionisti valga la seguente struttura:

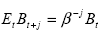(6.10)

per ogni j >0. Questa forma però rende possibile un aumento o un decremento di Bt potenzialmente illimitati, visto che tale componente varia con j, al tasso geometrico β^-1 che rappresenta l’autovalore dell’equazione e che come si è detto prima è maggiore dell’unità. Ma questo consentirebbe, in presenza di una bolla negativa, che dopo un numero finito di istanti j, il valore atteso dell’attività diventi negativo, e questo non può accadere. Dunque sarebbe da escludersi la componente bolla razionale negativa. A questo punto si fa riferimento alla seguente formulazione:

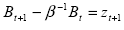(6.11)

dove z_t+1 è una variabile casuale generata da un processo stocastico tale che

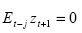per ogni j >0 (6.12)

Questa variabile contiene della nuova informazione disponibile in t+1 non legata ad F _t+1.Ciò che è importante di tale variabile è che il suo valore atteso è zero. La soluzione generale all' equazione di sopra, per ogni t è

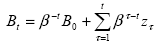(6.13)

le componenti della bolla razionale al tempo t sono due, di cui la prima è composta dal prodotto dell’autovalore elevato alla t per la componente bolla al tempo 0; la seconda componente è data dalla somma ponderata delle realizzazioni di zt da τ = 1 a τ = t. I pesi sono potenze dell’autovalore di modo che il contributo di zτ a Bt cresca esponenzialmente con la differenza tra τ e t.

L’impossibilità di una bolla razionale negativa, significa che la componente la componente bolla di un’azione al tempo t+1, oltre a soddisfare l’equazione (6.11) fa si che B _t+1 sia maggiore o uguale a zero. Ciò implica che

per ogni t ≥0 (6.14)

questo significa che z_t+1 è sempre grande abbastanza da garantire, nell’equazione (6.11) la non negatività di B _t+1 Infatti per Bt uguale a zero, il termine z_t+1 è non negativo in base alla (6.14), ed in particolare, come si evince dalla condizione (6.12), sarà proprio uguale a zero. In questo modo è dimostrato che se una bolla razionale non esiste al tempo t con t ≥ 0, allora non può nascere al tempo t+1, né in altra data successiva. Questo significa che se esiste una bolla razionale, si è formata nell’istante zero, cioè all’inizio della sua negoziazione.

Le critiche più diffuse ai modelli cui si è accennato sopra, riguardano il fatto che tali modelli falliscono nel fare distinzione tra l’ipotesi no-bubble e l’ipotesi che il modello testato sia specificato male (misspecification). In particolare avviene l’unione delle ipotesi no-bubble e no-misspecification, così che può succedere di scambiare come evidenza di una bolla speculativa l’errata specificazione del test. West (1987) ha proposto una procedura per separare l’ipotesi no-misspecification dall’ipotesi no-bubble, così che per diagnosticare una bolla si deve poter rigettare la seconda senza rigettare la prima.

Per fare questo, West ha combinato un test diretto per la specificazione, ed uno indiretto complicato per l’ipotesi no-bubble. Quest’ultimo è stato tuttavia oggetto di critiche in quanto ritenuto ambiguo. Poco dopo si è riusciti a superare questa difficoltà, in un test di Demirguc-Kunt e Dezhbakhsh (1988) in cui anche il test no-bubble veniva formalizzato con una procedura diretta. In questo stesso articolo[54] si nega l’evidenza di bolle speculative, al contrario dei risultati di West, raffrontando i due periodi 1871-1981 e 1871-1988.

Lo stesso risultato viene raggiunto da Santoni (1987): studiando i due mercati “bullish” degli anni ’20 e degli anni ’80, egli giunge alla conclusione che non c’è evidenza di autocorrelazione nei prezzi, e che quindi i rispettivi crash erano dovuti non allo scoppio di una bolla speculativa, quanto piuttosto a dei normali processi random walk. Sebbene l’analisi di correlazione, come si vedrà meglio nel capitolo 8, fornisca un metodo di indagine molto utile, è opinione di chi scrive che tali strumenti debbano essere necessariamente integrati con analisi di tipo sociale e storico perché ci si possa esprimere in merito a fenomeni particolari come le bolle speculative.

Tornando ai risultati dei test di Blanchard-Watson e Diba-Grossman, per quanto riguarda le bolle intrinseche nella prima data di contrattazione una forte evidenza deriva dalle IPO relative alle società tecnologiche durante il boom della new economy. La consapevolezza di tale sopravvalutazione implicita in questi debutti è così palese, che in questi ultimi tempi le maggiori banche d’affari del mondo brulicano di perquisizioni per aver “venduto” a taluni clienti la possibilità di partecipare all’acquisto di azioni al prezzo di emissione, su cui tutti sapevano fin dall’inizio che si sarebbero lucrate percentuali da capogiro[55].

Per quanto riguarda l’assenza di bolle negative, il meccanismo della retroazione psicologica visto nella parte seconda, sembra invece consentire fenomeni di vendita irrazionale, come quello che la commissione Brady diagnosticò a proposito del crollo dell’ottobre dell’87, sostenendo che la vendita quel giorno avveniva come risposta meccanica al ribasso, a prescindere dal livello dei prezzi[56].

54 Demirguc-Kunt, A., Dezhbakhsh, H. Testing For Speculative Bubbles in Stock Prices. Federal Reserve Bank of Cleveland, Working Paper 8807. 1988.

55 Si veda l’articolo di Federico Rampini Wall Street, Ormai è Operazione Mani Pulite. Pubblicato sull’inserto “Affari & Finanza” de La Repubblica, 29 Aprile 2002.

56 Report of the Presidential Task Force on Market Mechanisms (Brady Commission Report) Washington, D.C., 1988.

Marco Primavera

Successivo: Analisi Fondamentale

Sommario: Index