Test formali di correlazione: Durbin-Watson

Sebbene un andamento decrescente del correlogramma sia un buon modo di percepire la componente di trend, per accertare formalmente la stazionarietà si deve ricorrere a dei test formali, utili a verificare congiuntamente l’assenza di autocorrelazione seriale per più lag. Il test DW si usa nei modelli di regressione dei minimi quadrati per verificare l’ ipotesi nulla di indipendenza tra i residui del modello (ρ =0), contro l’ipotesi alternativa di autocorrelazione del primo ordine (ρ ≠ 0).

Serve dunque per verificare l’ assenza di un legame lineare tra ciascun residuo ed il precedente. La statistica di DW ha la seguente forma[64]:

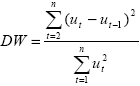(8.5.1)

In cui u_t è il residuo relativo al periodo t ed n è il numero delle osservazioni. Il DW è più efficace se espresso come test su

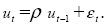
In questo caso se si accetta l’ ipotesi ρ = 0, il test da luogo ad un processo WN. Se 0<DW<2 allora l’ipotesi nulla H₀ è ρ=0, ovvero assenza di autocorrelazione e l’ipotesi alternativa H₁ è ? >0, ovvero autocorrelazione positiva di primo ordine.

Se 2<DW< 4 allora H₀ è ρ =0 e H₁ è ρ <0.

Il Q-Test di Ljung-Box

La stazionarietà di una serie, è stato visto, comporta l’ assenza di autocorrelazione seriale al variare del lag k: questo fa si che il valore assunto dalla serie in t non influenza il valore assunto in un istante successivo. Le ipotesi che si prendono di riferimento sono dunque: ρ_k =0 per ogni valore di k e ρ_k ≠0 per almeno un valore di k.

La statistica Q di Ljund-Box formalizza tali ipotesi nella seguente forma:

(8.6.1)

in cui n è la numerosità del campione. Ne consegue che per valori bassi di Q si dovrebbe rifiutare l’ipotesi di base di assenza di autocorrelazione seriale, mentre valori alti suggeriscono di accettare l’ipotesi alternativa, ovvero la non stazionarietà. Statisticamente parlando, almeno nell’ipotesi base, la statistica Q ha una distribuzione χ² .

I gradi di libertà della χ² sono dati dal numero delle autocorrelazioni meno il numero di termini autoregressivi meno i termini a media mobile. Se ad esempio la serie osservata è riconducibile ad un modello ARIMA(s,d,q), allora i gradi di libertà per la χ² saranno pari a s – d – q se si vuole verificare l’assenza di autocorrelazione seriale per k=1,2,…,s.

64 Si veda Greene, 1993, p 423-4

Marco Primavera

Successivo: L'analisi di cointegrazione

Sommario: Index