Analisi del trend

L’identifcazione di un trend può non essere complessa, laddove sia evidenziabile una precisa direzione, ad esempio verso l’alto. Tuttavia, in presenza di una componente di errore consistente, si dovrà innanzi tutto procedere allo smussamento. Un metodo di “smoothing” comunemente usato è quello che impiega le medie mobili, tramite cui si sostituisce ciascun elemento della serie con la media semplice o ponderata di un numero n di elementi circostanti, dove n rappresenta il grado di smussamento, o “smoothing window” (vi veda Box & Jenkins 1976).

Spesso al posto della media si ricorre anche alla mediana, la quale non da peso ad eventuali sbalzi tra i dati, anche se rende problematica la ponderazione in caso di sbalzi meno netti. In presenza di forti errori nella misurazione, si può ricorrere invece allo smussamento tramite i minimi quadrati ponderati in relazione alla distanza temporale, o allo smussamento ponderato negativamente in via esponenziale.

La maggior parte delle serie storiche monotone, possono essere approssimate da una funzione lineare. Se c’è una netta componente monotona non lineare, i dati devono essere trasformati per rimuovere la non linearità. Per questo scopo si utilizzano in genere funzioni logaritmiche o esponenziali.

L’analisi della stagionalità

La stagionalità è tecnicamente definita come una dipendenza da correlazione di ordine k tra ciascun i-esimo elemento della serie, e l’elemento (i-k)-esimo, ed è misurata tramite l’ autocorrelazione. Il termine k è detto ritardo (lag). In pratica se la componente di errore non è troppo elevata, la stagionalità può essere visualizzata come uno schema che si ripete ogni k elementi.

Per poter affrontare il concetto di analisi della correlazione si deve si deve fare riferimento ai momenti teorici dei processi stocastici, in particolare all’autocovarianza che si identifica come la covarianza tra valori della serie Z in istanti temporali diversi. Normalmente la covarianza misura la tendenza di due grandezze a variare nello stesso senso, in questo caso si utilizza un’unica variabile misurata in due istanti temporali diversi. In formule si ottiene:

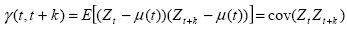(8.2.1)

Da notare che l’autocovarianza è funzione di due istanti temporali, t e (t+k). In questo senso la varianza risulta essere un caso particolare dell’autocovarianza, ponendo k=0. L’autocorrelazione ha il vantaggio, rispetto all’autocovarianza, di non essere compresa fra limiti fissi, ma tra i valori estremi di –1 e +1. L’autocorrelazione si ottiene semplicemente dividendo l’autocovarianza per il prodotto degli scarti quadratici medi di Z_t e Z_t-k .

La funzione di autocorrelazione (ACF) è il coefficiente di correlazione lineare ρ( κ) tra le variabili casuali Z_t e Z_t-k calcolato al variare di k.

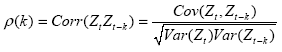(8.2.2)

I modelli stagionali di serie storiche possono essere esaminati tramite correlogrammi, i quali illustrano graficamente e numericamente la funzione di autocorrelazione (ACF), elencando i coefficienti di correlazione in serie (e i loro errori standard) per ritardi consecutivi in un intervallo specificato di ritardi (ad esempio, da 1 a 30).

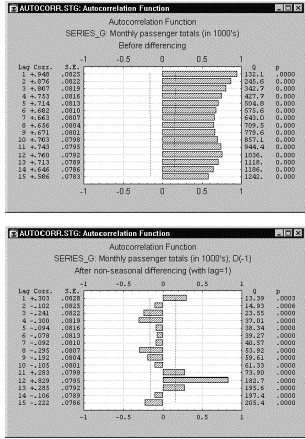
Figura 17. Esempio di correlogramma

Nell’esame dei correlogrammi si deve tenere presente che le autocorrelazioni per ritardi consecutivi sono formalmente dipendenti. Se il primo elemento è strettamente legato al secondo e questo ad un terzo, allora in qualche modo anche il primo ed il terzo sono collegati in qualche modo. Questo induce che lo schema di dipendenza seriale può cambiare sensibilmente eliminando l’autocorrelazione di primo livello (cioè differenziando la serie con un ritardo di 1).

Un altro modo di osservare dipendenze in serie è prendere in considerazione l’ autocorrelazione parziale (PACF). Essa rappresenta un’estensione della funzione di Autocorrelazione e viene definita come la correlazione lineare tra Z_t e Z_t-k al netto delle correlazioni lineari intermedie. (si veda anche McDowall, McCleary, Meidinger, & Hay, 1980). Sostanzialmente l’autocorrelazione parziale fornisce un quadro più nitido delle dipendenze seriali per singoli ritardi, eliminando le interferenze con altre dipendenze di serie.

Marco Primavera

Successivo: L'ipotesi di stazionarietà

Sommario: Index