Dall’analisi del comportamento dei rendimenti, Mandelbrot (1963) e Fama (1965) hanno evidenziato che ci sono periodi in cui la varianza tende a rimanere bassa ed altri periodi in cui tende a restare elevata. Altri studi hanno segnalato questo tipo di comportamento con evidenti implicazioni pratiche: shock sulla volatilità hanno ripercussioni sulla volatilità attesa futura. Per una definizione più precisa della persistenza della volatilità si considera il valore atteso della varianza per k periodi futuri:
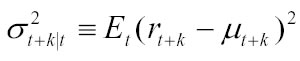
La previsione di volatilità dipende dall’insieme informativo a disposizione: shock sulla volatilità passata hanno ripercussioni sulla volatilità futura, il processo è quindi autocorrelato. La conseguenza principale, dal punto di vista statistico, è l’abbandono dell’ipotesi di una distribuzione comune dei rendimenti per individuare un modello in grado di descrivere l’evoluzione temporale della varianza condizionata.
Una misura formale di persistenza è stata suggerita da Engle e Patton (2001) come la derivata parziale della previsione della varianza condizionate di k periodi in avanti rispetto al valore assoluto del rendimento al quadrati del tempo t:
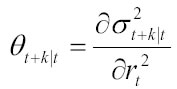
[1] [Mandelbrot] Matematico polacco che ha contribuito a mettere discussione alcuni consolidati fondamenti dell'economia classica e della finanza moderna, quali l'ipotesi di razionalità dei comportamenti degli agenti economici, l'ipotesi dell'efficienza del mercato, e quella secondo cui i movimenti dei prezzi di mercato sono descrivibili come un cammino casuale (random walk)
Successivo: 1.2.3 Ritorno in media della volatilità
Sommario: Index