Un ulteriore verifica che occorre fare è verificare che la varianza dell’errore di previsione sia compatibile con la varianza attesa. Per questo confronto ci si riconduce al classico modello di regressione lineare:
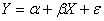con 
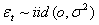
L’intero campione è composto da T osservazioni; stimando 2 modelli: uno per il campione di stima, composto da T-H osservazioni, e uno per il campione di previsione ex-post, composto da H osservazioni, si confrontano le 2 varianze ottenute e l’ipotesi nulla che riassume la stabilità numerica della varianza sarà:
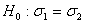
Tale ipotesi nulla può essere valutata con la statistica test, che confronta stime della variabilità entro e fuori il campione, che si distribuisce come un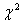 
con H gradi di libertà (in questo studio H=30):
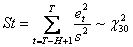
dove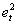 
è il quadrato del t-mo errore di previsione ad un passo e 
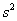è la stima della varianza nel campione con T-H osservazioni (campione di stima).
Dato che St= 17,88 e il valore soglia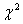 
con 30 gradi di libertà è di 43,77 (per α=0,05)
17,88<43,77
Poiché St<chi2(30) si ritiene di non rifiutare l’ipotesi nulla che riassume la stabilità numerica della varianza.
Successivo: 3.7 Previsori Alternativi: Un confronto
Sommario: Index