La letteratura interressata allo studio della volatilità

La ricerca e l’analisi di relazioni tra la volatilità dei prezzi e la volatilità implicita è stata ed è tutt’oggi al centro di grande attenzione da parte degli studiosi di econometria, finanza e statistica: articoli riguardanti questa applicazione sono stati affrontati da diversi autori In questa parte si vuole illustrare le variabili e i modelli interessati a questo tipo di studio: la vasta letteratura sul tema si caratterizza da un lato per il tentativo più o meno esplicito di spiegare e prevedere la volatilità sfruttando le informazioni sui rendimenti, dall’altro per il fatto di dedurre i modelli partendo da teorie economico finanziarie relative ai comportamenti di mercato.

La maggior parte degli studi sulla volatilità si concentrano sull’indice S&P500, sottolineando la sua importanza a livello mondiale come indice di riferimento dell’economia, per spiegare la volatilità vengono introdotte diverse variabili che possano influenzarla, e spesso viene portato in primo piano nell’analisi il VIX. Ad esempio Degiannakis e Floros (2010), utilizzano S&P500 e il VIX al quadrato,  dal 1990 al 2003, cercando un buon modello per spiegare la volatilità in modo da fare una migliore previsione: i modelli proposti sono GARCH, TGARCH e HYGARCH (tenendo conto dell’effetto asimmetrico della volatilità) tutti stimati a 1 solo ritardo:

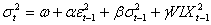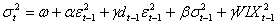1) 2) 3)

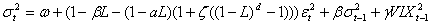
Secondo Blair, Poon e Taylor (2000), considerando rendimenti giornalieri dell’S&P100, e come variabili esogene per il modello dati VIX giornalieri al quadrato e rendimenti INTRADAY a 5 minuti dell’S&P100, dal 2 gennaio 1987 al 31 dicembre 1992 (inserendo una dummy dt per il “black Monday crash” nel 1987, in cui si registra un ribasso del -24%), il miglior modello stimato è un GJR GARCH(1,1) (Glosten, Jagannathan and Runkle 1993) che tiene conto della componente asimmetria, come segue:

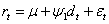
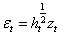
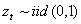
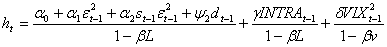
L’analisi procede inserendo una variabile alla volta per vedere come variano i coefficienti e cosa risulta più significativo. Nella’articolo di Hsu e Wu (2009), vengono utilizzati i rendimenti dell’indice TAIEX (che è il corrispondente dello S&P500 per il Taiwan) e il VIX calcolato sullo stesso indice, nello stesso modo come viene costruito dalla CBOE, vengono utilizzati dati al minuto dal 01/10/2008 al 19/01/2010, per un totale di 21680 osservazioni, divise in 3 periodi. In questo studio vengono usati i modelli GARCH, GJR e CGARCH (component GARCH) analizzati sia inserendo che non inserendo il VIX, confrontando i coefficienti per vedere se l’inserimento di questa variabile esogena è significativa. Anche in questo caso sono stimati modelli che tengono conto dell’asimmetria della volatilità. Modelli utilizzati sono tutti stimati a 1 ritardo:

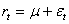
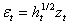
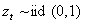
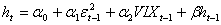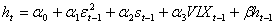1) 2) 3)  

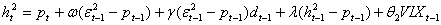
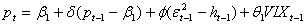
Tutti e 3 i modelli vengono stimati con e senza VIX, e poi sono confrontati tra di loro mediante le verosimiglianze e i punteggi AIC, per dimostrare se è significativo inserire il VIX per spiegare la volatilità.

G.Donaldson e M.Kamstra (2004) considerano rendimenti giornalieri e settimanali dell’S&P100 dal 1988 al 2003, i modelli econometrici utilizzati per l’analisi sono GARCH(1,1) e GJR(1,1): sono considerate come variabili esogene del modello il VIX e il volume di scambio del “New York Stock Exchange” (NYSE), che è la più grande borsa valori del mondo per volume di scambi e la seconda per numero di società quotate, ad avviso degli autori significativo a spiegare la volatilità dello S&P500.

Ahoniemi (2006) utilizza rendimenti giornalieri dello S&P500 e il rispettivo valore di volatilità implicita dal 1990 al 2004: lo studio affrontato consiste nel modellare la serie del VIX, utilizzando il suo valore in logaritmo, considerando come variabili esogene valori di chiusura del VIX ritardati, il volume di trading dello S&P500, l’indice MSCI EAFE (Europe, Australasian, Far East) che è utilizzato per misurare la performance del mercato azionario al di fuori di Stati Uniti e Canada, l’USD LIBOR a 3 mesi, U.S.

government bond yield e il prezzo del petrolio. Sulla base di test per l’autocorrelazione e il p-value dei coefficienti, un ARIMA(1,1,1) è risultato essere il migliore adattamento per la serie del log(VIX), il modello è stato poi migliorato stimando gli errori con un modello GARCH e inserendo le variabili esogene: la bontà di adattamento è stata confrontata principalmente con il Bayesian Information Criterion (BIC) e il coefficiente R2. Questa analisi è diversa dalle precedenti, ma è una riflessione importante su quali variabili possono spiegare la volatilità implicita, e per capire l’importanza del VIX, calcolato sullo S&P500, utile a spiegare la volatilità dei mercati finanziari.

Becker, Clements, Coleman-Fenn (2009) utilizzano dati giornalieri dal 1990 al 2008 dello S&P500 e i relativi dati VIX: per modellare la varianza sono impiegati GARCH(1,1) e GJR(1,1), anche in questo caso viene utilizzato un modello asimmetrico e uno simmetrico e vengono confrontate le stime ottenute. In tutti gli articoli affrontati si riscontra un effetto positivo del VIX sul modello, e la sua significatività nello studio della volatilità: è dimostrato, confrontando modelli con e senza VIX come variabile esogena, che questa variabile apporta dei punteggi più alti nell’accuratezza delle stime, e quindi si preferiscono sempre modelli in cui è considerata.

Mirko Cavallaro

Successivo: 2.2.1 L'importanza del VIX nelle previsioni

Sommario: Index