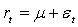Modello ARCH Auto-Regressive Conditional Heteroskedasticity

Considerando i rendimenti come:

1. Dato il set informativo It−1 = {εt−1, εt−2, . . . , εt−q}, il termine di disturbo εt segue un processo di tipo ARCH se sono verificate le seguenti condizioni:
2.  
3. 1. La media di εt condizionale al set informativo It−1 è nulla per ogni t.
4.  
5. 

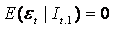
Ciò implica anche che E(εt) = 0 e soprattutto che tale processo risulti serialmente incorrelato condizionatamente allo stesso set informativo, infatti:

1.  
2. Cov(εt εt+k|It−h) = E(εt εt+k|It−h) − E(εt|It−h)E(εt+k|It−h)

Poichè per la legge dei valori attesi iterati E(εt|It−h) = E[E(εt|It−1)|It−h] = 0, risulta:

Cov(εt εt+k|It−h) = E(εt εt+k|It−h) Cov(εt εt+k|It−h) = E[E(εt εt+k|It+k−1)|It−h] Cov(εt εt+k|It−h) = E[εt · E(εt+k|It+k−1)|It−h]

Dato che E(εt+k|It+k−1) = 0 si ha: Cov(εt εt+k|It−h) = 0

2. La componente idiosincratica o innovazione εt è data dalla relazione:

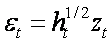
dove zt ~ i.i.d. (0, 1) è detto processo standardizzato. L’espressione suddetta rappresenta l’equazione di definizione dell’innovazione universalmente valida per qualsiasi modello di tipo ARCH: in base a questa espressione si assume che ε2t è un previsore corretto per la volatilità in quanto per definizione si ha:

1.  
2. ht = E(ε2t |It−1) = Var(εt |It−1)

Date queste premesse la distribuzione condizionale dell’innovazione risulta essere:

εt |It−1 ~ N(0, ht)

Da questa equazione emerge chiaramente che la varianza condizionale è variabile nel tempo. In sintesi un modello di regressione lineare sui rendimenti rt con innovazioni che seguono un modello di tipo ARCH si configura come segue:

Da questa equazione emerge chiaramente che la varianza condizionale è variabile nel tempo. In sintesi un modello di regressione lineare sui rendimenti rt con innovazioni che seguono un modello di tipo ARCH si configura come segue:

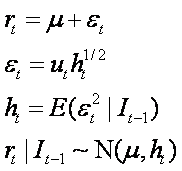
I modelli di tipo ARCH rappresentano quindi le espressioni analitiche per la varianza condizionale ht. Un importante elemento da evidenziare è il fatto che questi processi rappresentano lo strumento formale che mette in relazione le dinamiche (condizionali) della volatilità con il concetto di leptocurticità (non condizionale). Introdotto da Engle (1982), il modello ARCH specifica la varianza condizionale come una funzione lineare dei quadrati dei valori passati delle innovazioni, cioè:

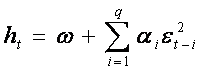
dove ω ≥ 0 e tutti gli αi ≥ 0 per i = 1, 2, . . . , q rappresentano i parametri da stimare.

L’espressione sopra riportata è l’equazione relativa alla innovazione εt che segue un generico processo ARCH(q) dove q è il numero di ritardi di ε2t. L’ARCH è quindi un processo con media nulla, varianza costante e varianza condizionale linearmente dipendente dai quadrati delle innovazioni. Esso riesce a catturare il fenomeno delle oscillazioni delle serie storiche relative ai rendimenti dei titoli, quindi interpreta il volatility clustering.

L’ARCH(q) di cui alla suddetta espressione può essere riscritto mediante un processo

MA(q) per i quadrati delle innovazioni, quindi:

1.  
2. ht = ω + A(L) ε2t

dove A(L) = α1L+ α2L2+. . .+ αqLq è il polinomio nell’operatore ritardo. Ponendo inoltre vt = ε2t − ht, l’ARCH(q) può essere riscritto anche come un modello AR(q) per i quadrati dei disturbi, cioè:

1.  
2. ε2t = ω + A(L) ε2t + vt

dove vt è un termine non normale, asimmetrico ed eteroschedastico con media condizionale nulla.

L’ARCH(q) è stazionario in covarianza quando le radici del polinomio 1 − A(L) cadono al di fuori del cerchio unitario. Ciò si traduce nella condizion

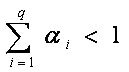
Se il processo è stazionario la varianza non condizionale dell’innovazione εt assume il seguente valore:

Mirko Cavallaro

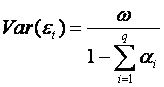
Successivo: 2.3.2 Modello GARCH- Generalized AutoRegressive Conditional Heteroskedasticity

Sommario: Index