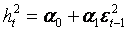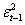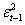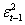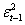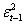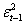Indice VIX, Volatilità, Modelli e Analisi Empirica
Robustezza del Modello Scelto
Per valutare se l’inserimento delle variabili considerate è significativo, è interessante il confronto con la stima dello stesso modello senza nessuna variabile esogena ossia un modello ARCH(1):
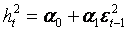
Si ottiene il seguente output di stima per l’intero intervallo considerato (2004-2010):
VARIABILI |
COEFFICIENTI |
C |
|
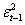
|
|
Figura 42: Stime coefficienti modello ARCH(1) senza VIX
VARIABILI |
COEFFICIENTI |
C |
|
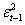
|
|
Figura 42: Stime coefficienti modello ARCH(1) senza VIX
Per valutare la significatività confronto i punteggi AIC dei 2 modelli:
ARCH(1) |
ARCH(1)+ VIXt-1+ VIX2t-1 |
|
|
Figura 43: Punteggi AIC modelli ARCH(1) e ARCH(1)+VIX+VIX2
Il valore del modello che include anche i dati VIX è nettamente minore (maggiore in valore assoluto), quindi si può affermare con certezza che è più significativo e modella meglio la varianza.
Dal momento che inserire il VIX aiuta a spiegare la variabilità del modello, per testarne la robustezza è interessante verificare come si comporta nel tempo, ossia se i coefficienti mantengono stessi segni e proporzioni, e relative probabilità, nei diversi anni considerati e ad intervalli di tempo più brevi. Se questo confronto risulterà significativo allora il modello si potrà considerare “buono”.
La costanza dei parametri sull’intervallo di stima, rappresenta una proprietà estremamente importante da valutare. Rappresenta infatti la base empirica per ipotizzare che le stime dei parametri, ottenute in funzione delle osservazioni disponibili, possono essere utili per costruire un buon previsore. Le relazioni fra variabili economiche spesso si modificano nel tempo e nello spazio; talvolta l’evoluzione dei parametri con cui vengono sintetizzate è lenta, talvolta molto veloce come, ad esempio, quando segue il presentarsi di eventi “eccezionali”. Se un modello mostra una forte instabilità nei parametri sull’intervallo di stima, difficilmente produrrà buone previsioni fuori dal campione (Guizzardi 2002, p.110).
Diventa così importante valutare il sentiero evolutivo delle stime dei parametri all’aumentare o al diminuire dell’intervallo campionario.
Per testare la robustezza del modello, vengono accorciati gli intervalli di stima e si valuta come si comportano i coefficienti, il procedimento è identico a quella già affrontato per la media:
- tenendo fissa la data finale dell’intervallo, anno 2010, si accorcia di un anno il periodo preso in considerazione
VARIABILI |
COEFFICIENTI |
|
2004-2010 |
2005-2010 |
2006-2010 |
2007-2010 |
2008-2010 |
2009-2010 |
C |
|
|
|
|
|
|
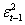
|
|
|
|
|
|
|
VIXt-1 |
|
|
|
|
|
|
VIX2t-1 |
|
|
|
|
|
|
Figura 44: Stime del modello ARCH(1)+VIX+VIX2 ad intervalli decrescenti
Dalle stime ottenute segni e proporzioni sono rispettati per i coefficienti nei diversi intervalli considerati, anche se non sempre le probabilità sono accettate.
- Stime con intervalli campionari di 3 anni
VARIABILI |
COEFFICIENTI |
|
2004-2007 |
2005-2008 |
2006-2009 |
2007-2010 |
C |
|
|
|
|
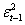
|
|
|
|
|
VIXt-1 |
|
|
|
|
VIX2t-1 |
|
|
|
|
Figura 45: Stime del modello ARCH(1)+VIX+VIX2 su intervalli di 3 anni
Anche in questo caso segni e proporzioni rimangono costanti nel tempo, anche se alcuni valori non sono accettati guardando le loro probabilità. Nel trimestre 2004-2007 il coefficiente della costante e del VIX hanno segni diversi dal resto delle stime, ma non è preoccupante questa informazione, può essere ricondotta a valori anomali di quotazioni in quel periodo.
- Stime con intervalli campionari di 2 anni
VARIABILI |
COEFFICIENTI |
|
2004-2006 |
2005-2007 |
2006-2008 |
2007-2009 |
2008-2010 |
C |
|
|
|
|
|
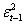
|
|
|
|
|
|
VIXt-1 |
|
|
|
|
|
VIX2t-1 |
|
|
|
|
|
Figura 46: Stime del modello ARCH(1)+VIX+VIX2 su intervalli di 2 anni
Allo stesso modo i seguenti valori hanno la stessa costanza nel segno e nelle proporzioni, con un valore diverso nel biennio 2005-2007 in cui gli errori hanno segno positivo rispetto agli altri intervalli.
- Stime con intervallo campionario di 1 anno
VARIABILI |
COEFFICIENTI |
|
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
C |
|
|
|
|
|
|
|
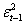
|
|
|
|
|
|
|
|
VIXt-1 |
|
|
|
|
|
|
|
VIX2t-1 |
|
|
|
|
|
|
|
Figura 47: Stime del modello ARCH(1)+VIX+VIX2 su intervalli di 1 anno
Con stime a 1 anno, si nota più diversità nella distribuzione dei segni dei coefficienti, anche se sono abbastanza proporzionali, ma soprattutto quasi tutti i dati sono rifiutati dalle rispettive probabilità. Questa informazione fa presupporre che il modello stimato sia migliore su un intervallo temporale più ampio, e che considerando 1 anno probabilmente non riesce a dare informazioni esaustive sui movimenti di mercato a breve termine.
Mirko Cavallaro
Successivo: 3.6 Le Previsioni
Sommario: Index